
如圖,已知直線 過點
過點 和
和 ,
, 是
是 軸正半軸上的動點,
軸正半軸上的動點,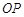 的垂直平分線交
的垂直平分線交 于點
于點 ,交
,交 軸于點
軸于點 .
.
(1)直接寫出直線 的解析式;
的解析式;
(2)當 時,設
時,設 ,
, 的面積為
的面積為 ,求S關于t的函數關系式;并求出S的最大值;
,求S關于t的函數關系式;并求出S的最大值;
(3)當點Q在線段AB上(Q與A、B不重合)時,直線 過點A且與x軸平行,問在
過點A且與x軸平行,問在 上是否存在點C,使得
上是否存在點C,使得 是以
是以 為直角頂點的等腰直角三角形?若存在,求出點C的坐標,并證明;若不存在,請說明理由.
為直角頂點的等腰直角三角形?若存在,求出點C的坐標,并證明;若不存在,請說明理由.
(1)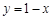 ;
;
(2)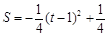 ,當
,當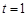 時,S有最大值
時,S有最大值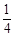 ;
;
(3)在 上存在點
上存在點 ,使得
,使得 是以
是以 為直角頂點的等腰直角三角形.
為直角頂點的等腰直角三角形.
解析試題分析:(1)已知直線L過A,B兩點,可將兩點的坐標代入直線的解析式中,用待定系數法求出直線L的解析式;
(2)求三角形OPQ的面積,就需知道底邊OP和高QM的長,已知了OP為t,關鍵是求出QM的長.已知了QM垂直平分OP,那么OM= ,
, ,再求即可;
,再求即可;
(3)如果存在這樣的點C,那么CQ=QP=OQ,因此C,O就關于直線BL對稱,因此C的坐標應該是(1,1).那么只需證明CQ⊥PQ即可.分情況進行討論.
試題解析:(1)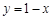 ;
;
(2)∵ ,∴Q點的橫坐標為
,∴Q點的橫坐標為 ,
,
當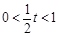 ,即
,即 時,
時, ,
,
∴ .
.
當 時,
時, ,
,
∴當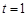 時,S有最大值
時,S有最大值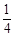 ;
;
(3)∵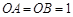 ,∴
,∴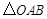 是等腰直角三角形,
是等腰直角三角形,
若在 上存在點
上存在點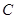 ,使得
,使得 是以
是以 為直角頂點的等腰直角三角形,則
為直角頂點的等腰直角三角形,則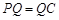 ,
,
∴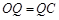 ,∵
,∵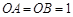 、
、 軸,∴
軸,∴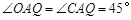
O、C關于直線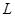 對稱∴
對稱∴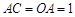 ,得
,得 .
.
連接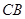 ,則四邊形
,則四邊形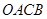 是正方形.
是正方形.
(i)當點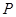 在線段
在線段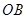 上,如圖–1.
上,如圖–1.
由對稱性,得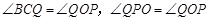 ,
,
∴ ,
,
∴ .
.
即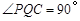
(ii)當點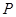 在線段
在線段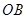 的延長線上,如圖–2,
的延長線上,如圖–2,
∵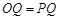 ∴
∴ 由對稱性可知
由對稱性可知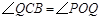
∴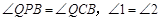 ,
,
∴ .
.
綜合(i)(ii),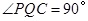 .
.
∴在 上存在點
上存在點 ,使得
,使得 是以
是以 為直角頂點的等腰直角三角形.
為直角頂點的等腰直角三角形.
考點:二次函數綜合題.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
如圖①,在平面直角坐標系中,點A是拋物線y=x2在第一象限上的一個點,連結OA,過點A作AB⊥OA,交y軸于點B,設點A的橫坐標為n.
【探究】:
(1)當n=1時,點B的縱坐標是 ;
(2)當n=2時,點B的縱坐標是 ;
(3)點B的縱坐標是 (用含n的代數式表示).
【應用】:
如圖②,將△OAB繞著斜邊OB的中點順時針旋轉180°,得到△BCO.
(1)求點C的坐標(用含n的代數式表示);
(2)當點A在拋物線上運動時,點C也隨之運動.當1≤n≤5時,線段OC掃過的圖形的面積是 .
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,拋物線y=ax2+ x+c與x軸交于點A(4,0)、B(-1,0),與y軸交于點C,連接AC,點M是線段OA上的一個動點(不與點O、A重合),過點M作MN∥AC,交OC于點N,將△OMN沿直線MN折疊,點O的對應點O′落在第一象限內,設OM=t,△O′MN與梯形AMNC重合部分面積為S.
x+c與x軸交于點A(4,0)、B(-1,0),與y軸交于點C,連接AC,點M是線段OA上的一個動點(不與點O、A重合),過點M作MN∥AC,交OC于點N,將△OMN沿直線MN折疊,點O的對應點O′落在第一象限內,設OM=t,△O′MN與梯形AMNC重合部分面積為S.
(1)求拋物線的解析式;
(2)①當點O′落在AC上時,請直接寫出此時t的值;
②求S與t的函數關系式;
(3)在點M運動的過程中,請直接寫出以O、B、C、O′為頂點的四邊形分別是等腰梯形和平行四邊形時所對應的t值.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
已知拋物線y=x2﹣(k+2)x+ 和直線y=(k+1)x+(k+1)2.
和直線y=(k+1)x+(k+1)2.
(1)求證:無論k取何實數值,拋物線總與x軸有兩個不同的交點;
(2)拋物線于x軸交于點A、B,直線與x軸交于點C,設A、B、C三點的橫坐標分別是x1、x2、x3,求x1•x2•x3的最大值;
(3)如果拋物線與x軸的交點A、B在原點的右邊,直線與x軸的交點C在原點的左邊,又拋物線、直線分別交y軸于點D、E,直線AD交直線CE于點G(如圖),且CA•GE=CG•AB,求拋物線的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,已知二次函數的圖象過點O(0,0),A(4,0),B(2,﹣ ),M是OA的中點.
),M是OA的中點.
(1)求此二次函數的解析式;
(2)設P是拋物線上的一點,過P作x軸的平行線與拋物線交于另一點Q,要使四邊形PQAM是菱形,求P點的坐標;
(3)將拋物線在x軸下方的部分沿x軸向上翻折,得曲線OB′A(B′為B關于x軸的對稱點),在原拋物線x軸的上方部分取一點C,連接CM,CM與翻折后的曲線OB′A交于點D.若△CDA的面積是△MDA面積的2倍,這樣的點C是否存在?若存在求出C點的坐標,若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,拋物線y=ax2+bx+c經過A(﹣3.0)、C(0,4),點B在拋物線上,CB∥x軸,且AB平分∠CAO.
(1)求拋物線的解析式;
(2)線段AB上有一動點P,過點P作y軸的平行線,交拋物線于點Q,求線段PQ的最大值;
(3)拋物線的對稱軸上是否存在點M,使△ABM是以AB為直角邊的直角三角形?如果存在,求出點M的坐標;如果不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,在平面直角坐標系中,已知點P(0,4),點A在線段OP上,點B在x軸正半軸上,且AP=OB=t, 0<t<4,以AB為邊在第一象限內作正方形ABCD;過點C、D依次向x軸、y軸作垂線,垂足為M,N,設過O,C兩點的拋物線為y=ax2+bx+c.
(1)填空:△AOB≌△ ≌△BMC(不需證明);用含t的代數式表示A點縱坐標:A(0, ;
(2)求點C的坐標,并用含a,t的代數式表示b;
(3)當t=1時,連接OD,若此時拋物線與線段OD只有唯一的公共點O,求a的取值范圍;
(4)當拋物線開口向上,對稱軸是直線 ,頂點隨著t的增大向上移動時,求t的取值范圍.
,頂點隨著t的增大向上移動時,求t的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,已知拋物線 (
( 為常數,且
為常數,且 )與
)與 軸從左至右依次交于A,B兩點,與
軸從左至右依次交于A,B兩點,與 軸交于點C,經過點B的直線
軸交于點C,經過點B的直線 與拋物線的另一交點為D.
與拋物線的另一交點為D.
(1)若點D的橫坐標為-5,求拋物線的函數表達式;
(2)若在第一象限的拋物線上有點P,使得以A,B,P為頂點的三角形與△ABC相似,求 的值;
的值;
(3)在(1)的條件下,設F為線段BD上一點(不含端點),連接AF,一動點M從點A出發,沿線段AF以每秒1個單位的速度運動到F,再沿線段FD以每秒2個單位的速度運動到D后停止. 當點F的坐標是多少時,點M在整個運動過程中用時最少?
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
在平面直角坐標系xOy中,直線y=kx(k為常數)與拋物線 交于A,B兩點,且A點在y軸左側,P點的坐標為(0,﹣4),連接PA,PB.有以下說法:
交于A,B兩點,且A點在y軸左側,P點的坐標為(0,﹣4),連接PA,PB.有以下說法:
①PO2=PA•PB;
②當k>0時,(PA+AO)(PB﹣BO)的值隨k的增大而增大;
③當 時,BP2=BO•BA;
時,BP2=BO•BA;
④△PAB面積的最小值為 .
.
其中正確的是 (寫出所有正確說法的序號)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com