
【題目】如圖,在平面直角坐標系中,四邊形 OABC 為菱形,點 C 的坐標為(4,0),∠AOC = 60°,垂直于 x 軸的直線 l 從 y 軸出發,沿 x 軸正方向以每秒 1 個單位長度的速度運動,設直線 l 與 菱形 OABC 的兩邊分別交與點 M、N(點 M 在點 N 的上方).
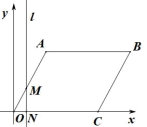
(1)求 A、B 兩點的坐標;
(2)設 OMN 的面積為 S,直線 l 運動時間為 t 秒(0 ≤t ≤6 ),試求 S 與 t 的函數表達 式;
(3)在題(2)的條件下,t 為何值時,S 的面積最大?最大面積是多少.
【答案】(1)A(2,![]() ),B(6,
),B(6,![]() );(2)當
);(2)當![]() 時,
時,![]() ;當
;當![]() ,
,![]() ;當
;當![]() 時,
時,![]() ;(3)
;(3)![]() 秒時,
秒時,![]() .
.
【解析】
(1)根菱形性質得出OA=AB=BC=CO=4,過A作AD⊥OC于D,求出AD、OD,即可得出答案;
(2)依題意可分為三種情況:①當0≤t≤2時,直線l與OA、OC兩邊相交,②當2<t≤4時,直線l與AB、OC兩邊相交,③當4<t≤6時,直線l與AB、BC兩邊相交,畫出圖形求出即可;
(3)根據(2)中各函數的性質和各自的自變量的取值范圍可得出S的最大值及對應的t的值.
解:(1)∵四邊形OABC為菱形,點C的坐標為(4,0),
∴![]()
過點A作![]() 于D.
于D.
∵![]()
∴![]() ,
,![]()
∴A(2,![]() ),B(6,
),B(6,![]() ).
).
(2)∵![]() ,
,
∴![]() ,
,
直線l從y軸出發,沿x軸正方向運動與菱形OABC的兩邊相交有三種情況:
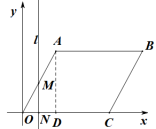
①當![]() 時,直線l與直線OA,OC兩邊相交,
時,直線l與直線OA,OC兩邊相交,
∴![]() ,
,
則![]() ;
;
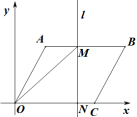
②當![]() 時,直線l與AB、OC兩邊相交,
時,直線l與AB、OC兩邊相交,
則![]() ;
;
③當![]() 時,直線l與AB、BC兩邊相交,
時,直線l與AB、BC兩邊相交,
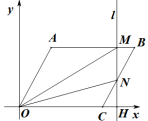
設直線l與x軸相交于H點,
∵![]() ,
,
∴![]() ;
;
綜上所述: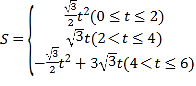 ,
,
(3)由(2)知,當![]() 時,
時,![]() ;
;
當![]() 時,
時,![]() ;
;
∵![]() 的對稱軸為
的對稱軸為![]() ,
,
∴函數![]() ,當
,當![]() 時,S隨
時,S隨![]() 的增大而減小,
的增大而減小,
即![]() 時,S取得最大值:
時,S取得最大值:![]() ,
,
綜上所述,當![]() 秒時,
秒時,![]() .
.


 智慧小復習系列答案
智慧小復習系列答案科目:初中數學 來源: 題型:
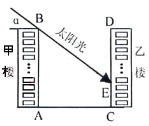
【題目】下圖為某小區的兩幢1O層住宅樓,由地面向上依次為第1層、第2層、…、第10層,每層的高度為3m,兩樓間的距離AC=30m.現需了解在某一時段內,甲樓對乙樓的采光的影響情況.假設某一時刻甲樓樓頂B落在乙樓的影子長EC=h,太陽光線與水平線的夾角為α.
(1)用含α的式子表示h;
(2)當α=30°時,甲樓樓頂B的影子落在乙樓的第幾層?從此時算起,若α每小時增加10°,幾小時后,甲樓的影子剛好不影響乙樓采光.
查看答案和解析>>
科目:初中數學 來源: 題型:
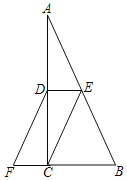
【題目】如圖,在△ABC中,∠ACB=90°,點D、E分別是AC、AB的中點,點F在BC的延長線上,且∠CDF=∠A.
(1)求證:四邊形DECF是平行四邊形;
(2)若∠A=30°,寫出圖中所有與FD長度相等的線段.
查看答案和解析>>
科目:初中數學 來源: 題型:
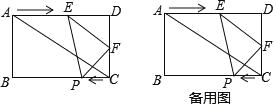
【題目】如圖,在矩形 ABCD 中,AB=6cm,AD=8cm,直線 EF 從點 A 出發沿 AD 方向勻速運動,速度是 2cm/s,運動過程中始終保持 EF∥AC.F 交
AD 于 E,交 DC 于點 F;同時,點 P 從點 C 出發沿 CB 方向勻速運動,速度是 1cm/s,連接 PE、PF,設運動時間 t(s)(0<t<4).
(1)當 t=1 時,求 EF 長;
(2)求 t 為何值時,四邊形 EPCD 為矩形;
(3)設△PEF 的面積為 S(cm2),求出面積 S 關于時間 t 的表達式;
(4)在運動過程中,是否存在某一時刻使 S△PC F:S 矩形 ABCD=3:16?若存在, 求出 t 的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在等邊![]() 中,
中,![]() ,點
,點![]() 在
在![]() 上,且
上,且![]() ,點
,點![]() 是
是![]() 上一動點,連接
上一動點,連接![]() ,將線段
,將線段![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 得到線段
得到線段![]() ,若要使點
,若要使點![]() 恰好在
恰好在![]() 上,則
上,則![]() 的長為().
的長為().
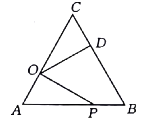
A. 4B. 5C. 6D. 8
查看答案和解析>>
科目:初中數學 來源: 題型:
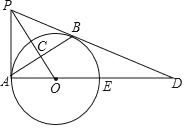
【題目】如圖,PB與⊙O相切于點B,過點B作OP的垂線BA,垂足為C,交⊙O于點A,連結PA,AO,AO的延長線交⊙O于點E,與PB的延長線交于點D.
(1)求證:PA是⊙O的切線;
(2)若tan∠BAD=![]() , 且OC=4,求PB的長.
, 且OC=4,求PB的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為監控某條生產線上產品的質量,檢測員每隔相同時間抽取一件產品,并測量其尺寸(![]() ),在一天的抽檢結束后,檢測員將測得的各數據按從小到大的順序整理成如下表格:
),在一天的抽檢結束后,檢測員將測得的各數據按從小到大的順序整理成如下表格:
編號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
尺寸 | 8.72 | 8.88 | 8.92 | 8.93 | 8.94 | 8.96 | 8.97 | 8.98 |
| 9.03 | 9.04 | 9.06 | 9.07 | 9.08 |
|
按照生產標準,產品等級規定如下:
尺寸(單位: | 產品等次 |
| 特等品 |
| 優等品 |
| 合格品 |
| 非合格品 |
注:在統計優等品個數時,將特等品計算在內;在統計合格個數時,將優等品(含特等品)算在內,
(1)已知此次抽檢的合格率為![]() ,請判斷編號為15的產品是否為合格品,并說明理由;
,請判斷編號為15的產品是否為合格品,并說明理由;
(2)已知此次及抽檢出的優等品尺寸的中位數為![]() .
.
①![]() __________;
__________;
②將這些優等品分成兩組,一組尺寸大于![]() ,另一種尺寸不大于
,另一種尺寸不大于![]() ,從這兩組中各隨機抽取1件進行復檢,求抽到的2件產品都是特等品的概率.
,從這兩組中各隨機抽取1件進行復檢,求抽到的2件產品都是特等品的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】周末,小明與小亮兩個人打算騎共享單車騎行出游,兩人打開手機APP進行選擇,已知附近共有3種品牌的5輛車,其中A品牌與B品牌各有2輛,C品牌有1輛,手機上無法識別品牌,且有人選中車后其他人無法再選.
(1)若小明首先選擇,則小明選中A品牌單車的概率為 ;
(2)求小明和小亮選中同一品牌單車的概率.(請用“畫樹狀圖”或“列表”的方法給出分析過程)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在A、B 兩地之間要修一條筆直的公路,從A地測得公路走向是北偏東48°,A,B兩地同時開工,若干天后公路準確接通,若公路AB長8千米,另一條公路BC長是6千米,且BC的走向是北偏西42°,則A地到公路BC的距離是( )
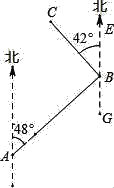
A. 6千米 B. 8千米 C. 10千米 D. 14千米
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com