
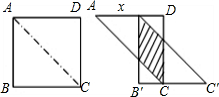
 設平移的距離為x(cm),兩個三角形重疊部分(陰影四邊形)的面積為S(cm2).
設平移的距離為x(cm),兩個三角形重疊部分(陰影四邊形)的面積為S(cm2). ?如果存在,請求出此時的平移距離x;如果不存在,請說明理由.
?如果存在,請求出此時的平移距離x;如果不存在,請說明理由.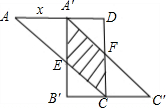 解:(1)由題意可知△ACD和△A′B′C′都為等腰直角三角形,且AD=2,
解:(1)由題意可知△ACD和△A′B′C′都為等腰直角三角形,且AD=2, (2-x),
(2-x), (2-x)=1:
(2-x)=1: 或x:
或x: (2-x)=
(2-x)= :1,
:1, ,
, 時,重疊部分的四邊形的相鄰兩邊之比為1:
時,重疊部分的四邊形的相鄰兩邊之比為1: .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:
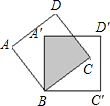 如圖,將邊長為2cm的兩個正方形紙片完全重合,按住其中一個不動,另一個繞點B順時針旋轉一個角度,若使重疊部分的面積為
如圖,將邊長為2cm的兩個正方形紙片完全重合,按住其中一個不動,另一個繞點B順時針旋轉一個角度,若使重疊部分的面積為4
| ||
| 3 |
| A、30° | B、35° |
| C、45° | D、60° |
查看答案和解析>>
科目:初中數學 來源: 題型:
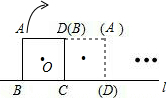 (2012•遵義)如圖,將邊長為
(2012•遵義)如圖,將邊長為| 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,將邊長為2cm的兩個互相重合的正方形紙片 按住其中一個不動,另一個紙點B順時針旋轉一個角度,若使重疊部分的面積為
如圖,將邊長為2cm的兩個互相重合的正方形紙片 按住其中一個不動,另一個紙點B順時針旋轉一個角度,若使重疊部分的面積為4
| ||
| 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com