
【題目】已知:如圖,點![]() ,
,![]() ,線段
,線段![]() 與
與![]() 軸平行,且
軸平行,且![]() ,拋物線
,拋物線![]()
(1)當![]() 時,求該拋物線與
時,求該拋物線與![]() 軸的交點坐標;
軸的交點坐標;
(2)當![]() 時,求
時,求![]() 的最大值(用含
的最大值(用含![]() 的代數式表示);
的代數式表示);
(3)當拋物線![]() 經過點
經過點![]() 時,
時,![]() 的解析式為__________,頂點坐標為__________,點
的解析式為__________,頂點坐標為__________,點![]() __________(填“是”或“否”)在
__________(填“是”或“否”)在![]() 上.
上.
若線段![]() 以每秒2個單位長的速度向下平移,設平移的時間為
以每秒2個單位長的速度向下平移,設平移的時間為![]() (秒).
(秒).
①若![]() 與線段
與線段![]() 總有公共點,求
總有公共點,求![]() 的取值范圍;
的取值范圍;
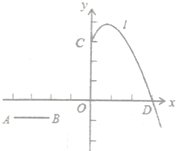
②若![]() 同時以每秒3個單位長的速度向下平移,
同時以每秒3個單位長的速度向下平移,![]() 在
在![]() 軸及其右側的圖象與直線
軸及其右側的圖象與直線![]() 總有兩個公共點,直接寫出
總有兩個公共點,直接寫出![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ,
,![]() ;(2)當
;(2)當![]() 時,
時, ![]() 有最大值0,當
有最大值0,當![]() 時,
時,![]() 有最大值
有最大值![]() ;(3)
;(3)![]() ,
,![]() ,否;①
,否;①![]() ;②
;②![]() .
.
【解析】
(1)當k=1時,該拋物線解析式y=x2-2x-3,y=0時,x2-2x-3=0,解得x1=-1,x2=3,該拋物線與x軸的交點坐標(-1,0),(3,0);
(2)拋物線y=kx2-2kx-3k的對稱軸直線x=![]() =1,當k>0時,x=3時,y有最大值,y最大值=9k-6k-3k=0,當k<0時,x=1時,y有最大值,y最大值=k-2k-3k=-4k;
=1,當k>0時,x=3時,y有最大值,y最大值=9k-6k-3k=0,當k<0時,x=1時,y有最大值,y最大值=k-2k-3k=-4k;
(3)當拋物線經過點C(0,3)時,拋物線的解析式為y=-x2+2x+3,頂點坐標(1,4),A(-4,-1),將x=-2代入y=-x2+2x+3,y=-5≠-1,點B不在l上;
①設平移后B(-2,-1-2t),A(-4,-1-2t),當拋物線經過點B時,有y=-5,當拋物線經過點A時,有y=-21,l與線段AB總有公共點,則-21≤-1-2t≤-5,解得2≤t≤10;
②平移過程中,設C(0,3-3t),則拋物線的頂點(1,4-3t),于是![]() ,解得4≤t<5.
,解得4≤t<5.
解:(1)當![]() 時,拋物線解析式為
時,拋物線解析式為![]() ,
,
當![]() 時,
時,![]() ,解得
,解得![]() ,
,![]() ,
,
所以該拋物線與![]() 軸的交點的坐標為
軸的交點的坐標為![]() ,
,![]() ,
,
(2)拋物線的對稱軸為直線![]() ,
,
當![]() 時,
時,![]() 時,
時,![]() ,
,![]() 有最大值0,
有最大值0,
當![]() 時,
時,![]() 時,
時,![]() ,
,![]() 有最大值
有最大值![]() ;
;
(3)![]() ,
,![]() 否;
否;
①設點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的坐標為
的坐標為![]() ,
,
當拋物線![]() 經過點
經過點![]() 時,有
時,有![]() ,
,
當拋物線![]() 經過點
經過點![]() 時,有
時,有![]() ,
,
當拋物線![]() 與線段
與線段![]() 總有公共點時,有
總有公共點時,有![]() ,
,
解得:![]() .
.
②![]() .
.


科目:初中數學 來源: 題型:
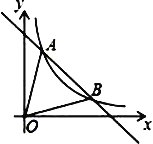
【題目】如圖,一次函數y=﹣x+5的圖象與反比例函數y=kx-1(k≠0)在第一象限的圖象交于A(1,n)和B兩點.
(1)求反比例函數的解析式與點B坐標;
(2)求△AOB的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知![]() 的直徑AB垂直弦CD于點E,過C點作CG∥AD交AB延長線于點G,連結CO并延長交AD于點F,且CF⊥AD.
的直徑AB垂直弦CD于點E,過C點作CG∥AD交AB延長線于點G,連結CO并延長交AD于點F,且CF⊥AD.
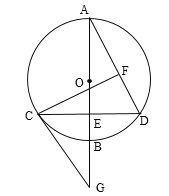
(1)求證:CG是⊙O的切線;
(2)若AB=4,求CD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,點O為坐標原點,直線y=﹣x+b交y軸于點A,交x軸于點B,S△AOB=![]() .
.
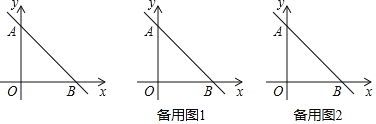
(1)求b的值;
(2)點C以每秒1個單位長度的速度從O點出發沿x軸向點B運動,點D以每秒2個單位長度的速度從A點出發沿y軸向點O運動,C,D兩點同時出發,當點D運動到點O時,C,D兩點同時停止運動.連接CD,設點C的運動時間為t秒,△CDO的面積為S,求S與t的函數關系式(不要求寫出自變量t的取值范圍);
(3)在(2)條件下,過點C作CE⊥CD交AB于點E,過點D作DF∥x軸交AB于點F,過點F作FH⊥CE,垂足為H.在CH上取點M,使得MH:HE=8:33,連接FM,若∠FMH=![]() ∠FEH,求t的值.
∠FEH,求t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
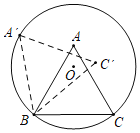
【題目】如圖,正![]() 的邊長為2,頂點
的邊長為2,頂點![]() 、
、![]() 在半徑為
在半徑為![]() 的圓上,頂點
的圓上,頂點![]() 在圓內,將正
在圓內,將正![]() 繞點
繞點![]() 逆時針旋轉,當點
逆時針旋轉,當點![]() 第一次落在圓上時,則點
第一次落在圓上時,則點![]() 運動的路線長為__________(結果保留
運動的路線長為__________(結果保留![]() );若
);若![]() 點落在圓上記做第1次旋轉,將
點落在圓上記做第1次旋轉,將![]() 繞點
繞點![]() 逆時針旋轉,當點
逆時針旋轉,當點![]() 第一次落在圓上記做第2次旋轉,再繞
第一次落在圓上記做第2次旋轉,再繞![]() 將
將![]() 逆時針旋轉,當點
逆時針旋轉,當點![]() 第一次落在圓上,記做第3次旋轉……,若此旋轉下去,當
第一次落在圓上,記做第3次旋轉……,若此旋轉下去,當![]() 完成第2018次旋轉時,
完成第2018次旋轉時,![]() 邊共回到原來位置__________次.
邊共回到原來位置__________次.
查看答案和解析>>
科目:初中數學 來源: 題型:
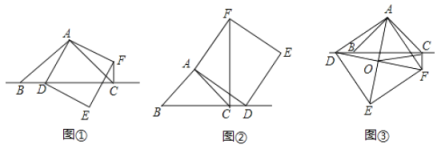
【題目】如圖,在等腰![]() 中,
中,![]() 點
點![]() 為直線
為直線![]() 上一動點(點
上一動點(點![]() 不與
不與![]() 、
、![]() 重合).以
重合).以![]() 為邊向右側作正方形
為邊向右側作正方形![]() ,連結
,連結![]() .
.
(猜想)如圖①,當點![]() 在線段
在線段![]() 上時,直接寫出
上時,直接寫出![]() 、
、![]() 、
、![]() 三條線段的數量關系.
三條線段的數量關系.
(探究)如圖②,當點![]() 在線段
在線段![]() 的延長線上時,判斷
的延長線上時,判斷![]() 、
、![]() 、
、![]() 三條線段的數量關系,并說明理由.
三條線段的數量關系,并說明理由.
(應用)如圖③,當點![]() 在線段
在線段![]() 的反向延長線上時,點
的反向延長線上時,點![]() 、
、![]() 分別在直線
分別在直線![]() 兩側,
兩側,![]() 、
、![]() 交點為點
交點為點![]() 連結
連結![]() ,若
,若![]() ,
,![]() ,則
,則![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,OD⊥弦BC于點F,交⊙O于點E,連接CE,AE,CD,若∠AEC=∠ODC.
(1)求證:直線CD為⊙O的切線;
(2)若AB=10,BC=8,則線段CD的長為 .

查看答案和解析>>
科目:初中數學 來源: 題型:
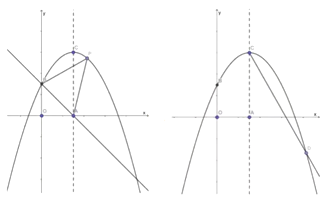
【題目】如圖所示,在平面直角坐標系中,拋物線![]() 的頂點坐標為
的頂點坐標為![]() ,并與
,并與![]() 軸交于點
軸交于點![]() ,點
,點![]() 是對稱軸與
是對稱軸與![]() 軸的交點.
軸的交點.
(1)求拋物線的解析式;
(2)如圖①所示, ![]() 是拋物線上的一個動點,且位于第一象限,連結BP、AP,求
是拋物線上的一個動點,且位于第一象限,連結BP、AP,求![]() 的面積的最大值;
的面積的最大值;
(3)如圖②所示,在對稱軸![]() 的右側作
的右側作![]() 交拋物線于點
交拋物線于點![]() ,求出
,求出![]() 點的坐標;并探究:在
點的坐標;并探究:在![]() 軸上是否存在點
軸上是否存在點![]() ,使
,使![]() ?若存在,求點
?若存在,求點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com