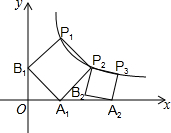
如圖,正方形A
1B
1P
1P
2的頂點P
1、P
2在反比例函數y=
(x>0)的圖象上,頂點A
1、B
1分別在x軸和y軸的正半軸上,再在其右側作正方形P
2P
3A
2B
2,頂點P
3在反比例函數y=
(x>0)的圖象上,頂點A
2在x軸的正半軸上,則P
2點的坐標為
(2,1)
(2,1)
,P
3的坐標為
.
分析:作P
1C⊥y軸于C,P
2D⊥x軸于D,P
3E⊥x軸于E,P
3F⊥P
2D于F,設P
1(a,
),則CP
1=a,OC=
,易得Rt△P
1B
1C≌Rt△B
1A
1O≌Rt△A
1P
2D,則OB
1=P
1C=A
1D=a,所以OA
1=B
1C=P
2D=
-a,則P
2的坐標為(
,
-a),然后把P
2的坐標代入反比例函數y=
,得到a的方程,解方程求出a,得到P
2的坐標;設P
3的坐標為(b,
),易得Rt△P
2P
3F≌Rt△A
2P
3E,則P
3E=P
3F=DE=
,通過OE=OD+DE=2+
=b,這樣得到關于b的方程,解方程求出b,得到P
3的坐標.
解答: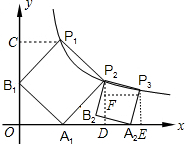
解:作P
1C⊥y軸于C,P
2D⊥x軸于D,P
3E⊥x軸于E,P
3F⊥P
2D于F,如圖,
設P
1(a,
),則CP
1=a,OC=
,
∵四邊形A
1B
1P
1P
2為正方形,
∴Rt△P
1B
1C≌Rt△B
1A
1O≌Rt△A
1P
2D,
∴OB
1=P
1C=A
1D=a,
∴OA
1=B
1C=P
2D=
-a,
∴OD=a+
-a=
,
∴P
2的坐標為(
,
-a),
把P
2的坐標代入y=
(x>0),得到(
-a)•
=2,解得a=-1(舍)或a=1,
∴P
2(2,1),
設P
3的坐標為(b,
),
又∵四邊形P
2P
3A
2B
2為正方形,
∴P
2P
3=P
3A
2,∠P
3EA
2=∠P
2FP
3,
∴Rt△P
2P
3F≌Rt△A
2P
3E,
∴P
3E=P
3F=DE=
,
∴OE=OD+DE=2+
,
∴2+
=b,解得b=1-
(舍),b=1+
,
∴
=
=
-1,
∴點P
3的坐標為 (
+1,
-1).
故答案為:(2,1),(
+1,
-1).
點評:本題考查了反比例函數圖象上點的坐標特點為橫縱坐標之積為定值;也考查了正方形的性質和三角形全等的判定與性質以及解分式方程的方法.
練習冊系列答案
相關習題
科目:初中數學
來源:
題型:
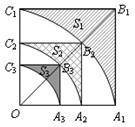
如圖,正方形OA
1B
1C
1的邊長為2,以O為圓心、OA
1為半徑作弧A
1C
1交OB
1于點B
2,設弧A
1C
1與邊A
1B
1、B
1C
1圍成的陰影部分面積S
1;然后以OB
2為對角線作正方形OA
2B
2C
2,又以O為圓心、OA
2為半徑作弧A
2C
2交OB
2于點B
3,設弧A
2C
2與邊A
2B
2、B
2C
2圍成的陰影部分面積為S
2;…,按此規律繼續作下去,設弧A
nC
n與邊A
nB
n、B
nC
n圍成的陰影部分面積為S
a.則S
1=
,S
2=
,…,S
n=
.
查看答案和解析>>
科目:初中數學
來源:2011-2012學年遼寧省盤錦市四完中九年級(上)第四次月考數學試卷(解析版)
題型:填空題
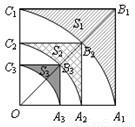
如圖,正方形OA
1B
1C
1的邊長為2,以O為圓心、OA
1為半徑作弧A
1C
1交OB
1于點B
2,設弧A
1C
1與邊A
1B
1、B
1C
1圍成的陰影部分面積S
1;然后以OB
2為對角線作正方形OA
2B
2C
2,又以O為圓心、OA
2為半徑作弧A
2C
2交OB
2于點B
3,設弧A
2C
2與邊A
2B
2、B
2C
2圍成的陰影部分面積為S
2;…,按此規律繼續作下去,設弧A
nC
n與邊A
nB
n、B
nC
n圍成的陰影部分面積為S
a.則S
1=
,S
2=
,…,S
n=
.

查看答案和解析>>
科目:初中數學
來源:2009-2010學年浙江省麗水市蓮都區九年級(上)第三次月考數學試卷(解析版)
題型:填空題
如圖,正方形OA
1B
1C
1的邊長為2,以O為圓心、OA
1為半徑作弧A
1C
1交OB
1于點B
2,設弧A
1C
1與邊A
1B
1、B
1C
1圍成的陰影部分面積S
1;然后以OB
2為對角線作正方形OA
2B
2C
2,又以O為圓心、OA
2為半徑作弧A
2C
2交OB
2于點B
3,設弧A
2C
2與邊A
2B
2、B
2C
2圍成的陰影部分面積為S
2;…,按此規律繼續作下去,設弧A
nC
n與邊A
nB
n、B
nC
n圍成的陰影部分面積為S
a.則S
1=
,S
2=
,…,S
n=
.
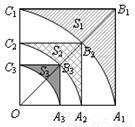
查看答案和解析>>
科目:初中數學
來源:2010年北京市東城區中考數學二模試卷(解析版)
題型:填空題
如圖,正方形OA
1B
1C
1的邊長為2,以O為圓心、OA
1為半徑作弧A
1C
1交OB
1于點B
2,設弧A
1C
1與邊A
1B
1、B
1C
1圍成的陰影部分面積S
1;然后以OB
2為對角線作正方形OA
2B
2C
2,又以O為圓心、OA
2為半徑作弧A
2C
2交OB
2于點B
3,設弧A
2C
2與邊A
2B
2、B
2C
2圍成的陰影部分面積為S
2;…,按此規律繼續作下去,設弧A
nC
n與邊A
nB
n、B
nC
n圍成的陰影部分面積為S
a.則S
1=
,S
2=
,…,S
n=
.
查看答案和解析>>
科目:初中數學
來源:2010年浙江省杭州市蕭山區中考數學模擬試卷47(河莊鎮中 陳國亞)(解析版)
題型:填空題
(2010•東城區二模)如圖,正方形OA
1B
1C
1的邊長為2,以O為圓心、OA
1為半徑作弧A
1C
1交OB
1于點B
2,設弧A
1C
1與邊A
1B
1、B
1C
1圍成的陰影部分面積S
1;然后以OB
2為對角線作正方形OA
2B
2C
2,又以O為圓心、OA
2為半徑作弧A
2C
2交OB
2于點B
3,設弧A
2C
2與邊A
2B
2、B
2C
2圍成的陰影部分面積為S
2;…,按此規律繼續作下去,設弧A
nC
n與邊A
nB
n、B
nC
n圍成的陰影部分面積為S
a.則S
1=
,S
2=
,…,S
n=
.

查看答案和解析>>

 如圖,正方形A1B1P1P2的頂點P1、P2在反比例函數y=
如圖,正方形A1B1P1P2的頂點P1、P2在反比例函數y= 解:作P1C⊥y軸于C,P2D⊥x軸于D,P3E⊥x軸于E,P3F⊥P2D于F,如圖,
解:作P1C⊥y軸于C,P2D⊥x軸于D,P3E⊥x軸于E,P3F⊥P2D于F,如圖,

 如圖,正方形OA1B1C1的邊長為2,以O為圓心、OA1為半徑作弧A1C1交OB1于點B2,設弧A1C1與邊A1B1、B1C1圍成的陰影部分面積S1;然后以OB2為對角線作正方形OA2B2C2,又以O為圓心、OA2為半徑作弧A2C2交OB2于點B3,設弧A2C2與邊A2B2、B2C2圍成的陰影部分面積為S2;…,按此規律繼續作下去,設弧AnCn與邊AnBn、BnCn圍成的陰影部分面積為Sa.則S1=
如圖,正方形OA1B1C1的邊長為2,以O為圓心、OA1為半徑作弧A1C1交OB1于點B2,設弧A1C1與邊A1B1、B1C1圍成的陰影部分面積S1;然后以OB2為對角線作正方形OA2B2C2,又以O為圓心、OA2為半徑作弧A2C2交OB2于點B3,設弧A2C2與邊A2B2、B2C2圍成的陰影部分面積為S2;…,按此規律繼續作下去,設弧AnCn與邊AnBn、BnCn圍成的陰影部分面積為Sa.則S1=


