
【題目】如圖1,將一個邊長為a厘米的正方形紙片剪去兩個小矩形,得到圖案,如圖2所示,再將剪下的兩個小矩形拼成一個新的矩形,如圖3所示:
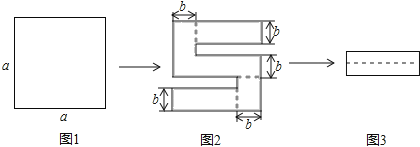
(1)列式表示新矩形的周長為______厘米(化到最簡形式)
(2)如果正方形紙片的邊長為8厘米,剪去的小矩形的寬為1厘米,那么所得圖形的周長為______厘米.
科目:初中數學 來源: 題型:
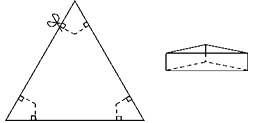
【題目】如圖,以邊長為20cm的正三角形紙板的各頂點為端點,在各邊上分別截取4cm長的六條線段,過截得的六個端點作所在邊的垂線,形成三個有兩個直角的四邊形.把它們沿圖中 虛線剪掉,用剩下的紙板折成一個底為正三角形的無蓋柱形盒子,則它的容積為________cm3 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】7張如圖1的長為a,寬為b(a>b)的小長方形紙片,按圖2的方式不重疊地放在矩形ABCD內,未被覆蓋的部分(兩個矩形)用陰影表示.設左上角與右下角的陰影部分的面積的差為S,當BC的長度變化時,按照同樣的放置方式,S始終保持不變,則a,b滿足( )
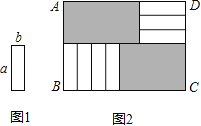
A.a=![]() bB.a=3bC.a=
bB.a=3bC.a=![]() bD.a=4b
bD.a=4b
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知△ABC中,a、b、c分別是∠A、∠B、∠C的對邊,下列條件不能判斷△ABC是直角三角形的是( )
A.∠A﹣∠B=∠C
B.∠A:∠B:∠C=3:4:5
C.(b+c)(b﹣c)=a2
D.a=7,b=24,c=25
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,AB=6,∠DAB=60°,AE分別交BC、BD于點E、F,CE=2,連接CF,以下結論:①△ABF≌△CBF;②點E到AB的距離是2![]() ;③tan∠DCF=
;③tan∠DCF=![]() ;④△ABF的面積為
;④△ABF的面積為![]() .其中一定成立的有幾個( )
.其中一定成立的有幾個( )
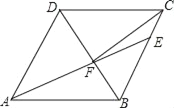
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
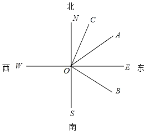
【題目】如圖,直線SN為南北方向,OB的方向是南偏東60°,∠SOB與∠NOC互余,OA平分∠BON.
(1)射線OC的方向是 .
(2)求∠AOC的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在正方形ABCD中,動點E,F分別從D,C兩點同時出發,以相同的速度在直線DC,CB上移動.
(1)如圖1,當點E在邊DC上自D向C移動,同時點F在邊CB上自C向B移動時,連接AE和DF交于點P,請你寫出AE與DF的數量關系和位置關系,并說明理;
(2)如圖2,當E,F分別在邊CD,BC的延長線上移動時,連接AE,DF,(1)中的結論還成立嗎?(請你直接回答“是”或“否”,不需證明);連接AC,求△ACE為等腰三角形時CE:CD的值;
(3)如圖3,當E,F分別在直線DC,CB上移動時,連接AE和DF交于點P,由于點E,F的移動,使得點P也隨之運動,請你畫出點P運動路徑的草圖.若AD=2,試求出線段CP的最大值.

圖1 圖2 圖3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+6x+c交x軸于A,B兩點,交y軸于點C.直線y=x﹣5經過點B,C.
(1)求拋物線的解析式;
(2)過點A的直線交直線BC于點M.
①當AM⊥BC時,過拋物線上一動點P(不與點B,C重合),作直線AM的平行線交直線BC于點Q,若以點A,M,P,Q為頂點的四邊形是平行四邊形,求點P的橫坐標;
②連接AC,當直線AM與直線BC的夾角等于∠ACB的2倍時,請直接寫出點M的坐標.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com