
【題目】定義:如圖1,點(diǎn)M,N把線段AB分割成AM,MN和BN,若以AM,MN,BN為邊的三角形是一個直角三角形,則稱點(diǎn)M,N是線段AB的勾股分割點(diǎn).
(1)已知點(diǎn)M,N是線段AB的勾股分割點(diǎn),若AM=2,MN=3,則BN=;
(2)如圖2,在△ABC中,F(xiàn)G是中位線,點(diǎn)D,E是線段BC的勾股分割點(diǎn),且EC>DE≥BD,連接AD,AE分別交FG于點(diǎn)M,N,求證:點(diǎn)M,N是線段FG的勾股分割點(diǎn);
(3)如圖3,已知點(diǎn)M,N是線段AB的勾股分割點(diǎn),MN>AM≥BN,四邊形AMDC,四邊形MNFE和四邊形NBHG均是正方形,點(diǎn)P在邊EF上,試探究S△ACN , S△APB , S△MBH的數(shù)量關(guān)系.
S△ACN=;S△MBH=;S△APB=;
S△ACN , S△APB , S△MBH的數(shù)量關(guān)系是 . 
【答案】
(1)![]() 或
或 ![]()
(2)證明∵點(diǎn)F、M、N、G分別是AB、AD、AE、AC邊上的中點(diǎn),
∴FM、MN、NG分別是△ABD、△ADE、△AEC的中位線,
∴BD=2FM,DE=2MN,EC=2NG,
∵點(diǎn)D,E是線段BC的勾股分割點(diǎn),且EC>DE>BD,
∴EC2=DE2+DB2,
∴4NG2=4MN2+4FM2,
∴NG2=MN2+FM2,
∴點(diǎn)M,N是線段FG的勾股分割點(diǎn)
(3)![]() ?AM2+
?AM2+ ![]() MN?AM,
MN?AM,![]() ?BN2+
?BN2+ ![]() ?MN?BN,
?MN?BN,![]() MN2+
MN2+ ![]() ?MN?AM+
?MN?AM+ ![]() ?MN?BN,S△APB=S△ACN+S△MBH
?MN?BN,S△APB=S△ACN+S△MBH
【解析】解:(1)分兩種情況:
①當(dāng)MN為最大線段時,
∵點(diǎn) M、N是線段AB的勾股分割點(diǎn),
∴BN= ![]() =
= ![]() =
= ![]() ;
;
②當(dāng)BN為最大線段時,
∵點(diǎn)M、N是線段AB的勾股分割點(diǎn),
∴BN= ![]() =
= ![]() =
= ![]() ;
;
綜上所述:BN的長為 ![]() 或
或 ![]() .
.
⑶∵四邊形AMDC,四邊形MNFE和四邊形NBHG均是正方形,
∴S△ACN= ![]() (AM+MN)AC=
(AM+MN)AC= ![]() (AM+MN)AM=
(AM+MN)AM= ![]() AM2+
AM2+ ![]() MNAM,
MNAM,
S△MBH= ![]() (MN+BN)BH=
(MN+BN)BH= ![]() (MN+BN)BN=
(MN+BN)BN= ![]() BN2+
BN2+ ![]() MNBN,
MNBN,
S△PAB= ![]() (AM+NM+BN)FN=
(AM+NM+BN)FN= ![]() (AM+MN+BN)MN=
(AM+MN+BN)MN= ![]() MN2+
MN2+ ![]() MNAM+
MNAM+ ![]() MNBN,
MNBN,
∴S△APB=S△ACN+S△MBH,
所以答案是S△APB=S△ACN+S△MBH.
【考點(diǎn)精析】關(guān)于本題考查的相似三角形的性質(zhì),需要了解對應(yīng)角相等,對應(yīng)邊成比例的兩個三角形叫做相似三角形才能得出正確答案.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
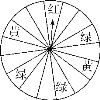
【題目】端午節(jié)期間,某商場為了吸引顧客,設(shè)立了一個可以自由轉(zhuǎn)動的轉(zhuǎn)盤(轉(zhuǎn)盤被平均分成16份),并規(guī)定:顧客每購買100元的商品,就能獲得一次轉(zhuǎn)轉(zhuǎn)盤的機(jī)會,如果轉(zhuǎn)盤停止后,指針正好對準(zhǔn)紅色、黃色或綠色區(qū)域,顧客就可以分別獲得玩具熊、童話書、水彩筆.小明和媽媽購買了125元的商品,請你回答下列問題:
(1)小明獲得獎品的概率是多少?
(2)小明獲得玩具熊、童話書、水彩筆的概率分別是多少?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知直線![]() .
.



(1)如圖1,直接寫出![]() ,
,![]() 和
和![]() 之間的數(shù)量關(guān)系.
之間的數(shù)量關(guān)系.
(2)如圖2,![]() ,
,![]() 分別平分
分別平分![]() ,
,![]() ,那么
,那么![]() 和
和![]() 有怎樣的數(shù)量關(guān)系?請說明理由.
有怎樣的數(shù)量關(guān)系?請說明理由.
(3)若點(diǎn)E的位置如圖3所示,![]() ,
,![]() 仍分別平分
仍分別平分![]() ,
,![]() ,請直接寫出
,請直接寫出![]() 和
和![]() 的數(shù)量關(guān)系.
的數(shù)量關(guān)系.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】綜合題化簡及計(jì)算
(1)化簡: ![]() ﹣
﹣ ![]()
(2)關(guān)于x的一元二次方程kx2﹣2x+3=0有兩個不相等的實(shí)數(shù)根.求:k的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為了加強(qiáng)學(xué)生的安全意識,某校組織了學(xué)生參加安全知識競賽,從中抽取了部分學(xué)生成績(得分?jǐn)?shù)取正整數(shù),滿分為100分)進(jìn)行統(tǒng)計(jì),繪制統(tǒng)計(jì)圖如下(未完成),解答下列問題:


(1)若A組的頻數(shù)比B組小24,求頻數(shù)分布直方圖中的![]() 、
、![]() 的值;
的值;
(2)扇形統(tǒng)計(jì)圖中,D部分所對的圓心角為n°,求n的值并補(bǔ)全頻數(shù)分布直方圖;
(3)若成績在80分以上為優(yōu)秀,全校共有2000名學(xué)生,估計(jì)成績優(yōu)異的學(xué)生有多少名?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,矩形OABC的兩條邊OA、OC分別在y軸和x軸上,已知點(diǎn)A(0,3)、點(diǎn)C(-4,0).
(1)若把矩形OABC沿直線DE折疊,使點(diǎn)C落在點(diǎn)A處,直線DE與OC、AC、AB的交點(diǎn)分別為D、F、E,求折痕DE的長;
(2)若點(diǎn)P在x軸上,在平面內(nèi)是否存在點(diǎn)Q,使以P、D、E、Q為頂點(diǎn)的四邊形是菱形?若存在,則請直接寫出點(diǎn)Q的坐標(biāo);若不存在,請說明理由;
(3)如圖2,若M為AC邊上的一動點(diǎn),在OA上取一點(diǎn)N(0,1),將矩形OABC繞點(diǎn)O順時針旋轉(zhuǎn)一周,在旋轉(zhuǎn)的過程中,M的對應(yīng)點(diǎn)為M1,請直接寫出NM1的最大值和最小值.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在南通市中小學(xué)標(biāo)準(zhǔn)化建設(shè)工程中,某校計(jì)劃購進(jìn)一批電腦和電子白板,經(jīng)過市場考察得知,購買![]() 臺電腦和
臺電腦和![]() 臺電子白板需要
臺電子白板需要![]() 萬元,購買
萬元,購買![]() 臺電腦和
臺電腦和![]() 臺電子白板需要
臺電子白板需要![]() 萬元.
萬元.
(1)求每臺電腦、每臺電子白板各多少萬元;
(2)根據(jù)學(xué)校實(shí)際,需購進(jìn)電腦和電子白板共![]() 臺,若總費(fèi)用不超過
臺,若總費(fèi)用不超過![]() 萬元,則至多購買電子白板多少臺?
萬元,則至多購買電子白板多少臺?
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com