
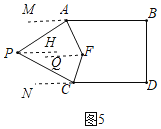
【題目】◆探索發現:如圖是一種網紅彈弓的實物圖,在兩頭上系上皮筋,拉動皮筋可形成平面示意圖如圖1、圖2,彈弓的兩邊可看成是平行的,即![]() .各活動小組探索
.各活動小組探索![]() 與
與![]() ,
,![]() 之間的數量關系.已知
之間的數量關系.已知![]() ,點
,點![]() 不在直線
不在直線![]() 和直線
和直線![]() 上.在圖1中,智慧小組發現:
上.在圖1中,智慧小組發現:![]() ;
;

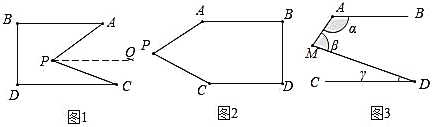
智慧小組是這樣思考的:過點![]() 作
作![]() ,……
,……
請你按照智慧小組作的輔助線補全推理過程.
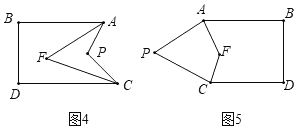
◆類比思考:①在圖2中,![]() 與
與![]() ,
,![]() 之間的數量關系為________.
之間的數量關系為________.
②如圖3,已知![]() ,則角
,則角![]() 、
、![]() 、
、![]() 之間的數量關系為________.
之間的數量關系為________.
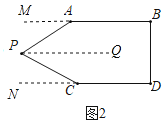
◆解決問題:善思小組提出:如圖4,圖5.![]() ,
,![]() ,
,![]() 分別平分
分別平分![]() ,
,![]() .
.
①在圖4中,![]() 與
與![]() 之間的關系為________.
之間的關系為________.
②在圖5中,![]() 與
與![]() 之間的關系為________.
之間的關系為________.
【答案】探索發現:見解析;類比思考:①![]() ;②
;②![]() ;解決問題:①
;解決問題:①![]() ;②
;②![]() .
.
【解析】
探索:發現由平行線的性質得出∠APQ=∠A,由PQ∥AB,AB∥CD,推出PQ∥CD,得出∠APQ=∠C,推出∠APQ+∠CPQ=∠A+∠C,即可得出結論;
類比思考①過點P作PQ∥AB,延長BA到M,延長DC到N,由平行線的性質得出∠APQ=∠PAM,由PQ∥AB,AB∥CD,推出PQ∥CD,得出∠APQ=∠PCN,則∠APQ+∠CPQ+∠PAB+∠PCD=360°,即可得出結果;
②過點M作MQ∥AB,由平行線的性質得出α+∠QMA=180°,由MQ∥AB,AB∥CD,推出MQ∥CD,得出∠QMD=γ,即可得出結果;
解決問題①過點P作PQ∥AB,過點F作FM∥AB,由平行線的性質得出∠APQ=∠BAP,∠AFM=∠BAF,由角平分線的性質得出∠BAF=∠PAF,即∠AFM=![]() ∠BAP,由PQ∥AB,FM∥AB,AB∥CD,推出PQ∥CD,FM∥CD,得出∠CPQ=∠DCP,∠CFM=∠DCF,由角平分線的性質得出∠DCF=∠PCF,即∠CFM=
∠BAP,由PQ∥AB,FM∥AB,AB∥CD,推出PQ∥CD,FM∥CD,得出∠CPQ=∠DCP,∠CFM=∠DCF,由角平分線的性質得出∠DCF=∠PCF,即∠CFM=![]() ∠DCP,推出∠APC=∠BAP+∠DCP,∠AFC=
∠DCP,推出∠APC=∠BAP+∠DCP,∠AFC=![]() (∠BAP+∠DCP),即可得出結果;
(∠BAP+∠DCP),即可得出結果;
②過點P作PH∥AB,過點F作FQ∥AB,延長BA到M,延長DC到N,由平行線的性質得出∠APH=∠MAP,∠AFQ=∠BAF,由角平分線的性質得出∠BAF=∠PAF,即2∠AFQ=∠BAP,由PH∥AB,FQ∥AB,AB∥CD,推出PH∥CD,FQ∥CD,得出∠CPH=∠NCP,∠CFQ=∠DCF,由角平分線的性質得出∠DCF=∠PCF,即2∠CFQ=∠DCP,由∠BAP+∠MAP=180°,∠DCP+∠NCP=180°,得出2∠AFQ+∠APH=180°,2∠CFQ+∠CPH=180°,即可得出結果.
探索發現:
∴![]()
∵![]() 、
、![]()
∴![]()
∴![]()
∴![]()
即![]()
類比思考:①∠APC+∠A+∠C=360°;理由如下:
過點P作PQ∥AB,延長BA到M,延長DC到N,如圖2所示:
∴∠APQ=∠PAM,
∵PQ∥AB,AB∥CD,
∴PQ∥CD,
∴∠APQ=∠PCN,
∴∠APQ+∠CPQ+∠PAB+∠PCD=180°+180°=360°,
∴∠APC+∠A+∠C=360°,
故答案為:∠APC+∠A+∠C=360°;

②α+β-γ=180°;理由如下:
過點M作MQ∥AB,如圖3所示:
∴α+∠QMA=180°,
∵MQ∥AB,AB∥CD,
∴MQ∥CD,
∴∠QMD=γ,
∵∠QMA+∠QMD=β,
∴α+β-γ=180°,
故答案為:α+β-γ=180°;
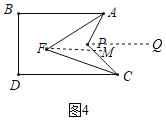
解決問題:①∠AFC=![]() ∠APC;理由如下:
∠APC;理由如下:
過點P作PQ∥AB,過點F作FM∥AB,如圖4所示:
∴∠APQ=∠BAP,∠AFM=∠BAF,
∵AF平分∠BAP,
∴∠BAF=∠PAF,
∴∠AFM=![]() ∠BAP,
∠BAP,
∵PQ∥AB,FM∥AB,AB∥CD,
∴PQ∥CD,FM∥CD,
∴∠CPQ=∠DCP,∠CFM=∠DCF,
∵CF平分∠DCP,
∴∠DCF=∠PCF,
∴∠CFM=![]() ∠DCP,
∠DCP,
∴∠APC=∠BAP+∠DCP,∠AFC=![]() ∠BAP+
∠BAP+![]() ∠DCP=
∠DCP=![]() (∠BAP+∠DCP),
(∠BAP+∠DCP),
∴∠AFC=![]() ∠APC,
∠APC,
故答案為:∠AFC=![]() ∠APC;
∠APC;
②∠AFC=180°-![]() ∠APC;理由如下:
∠APC;理由如下:
過點P作PH∥AB,過點F作FQ∥AB,延長BA到M,延長DC到N,如圖5所示:
∴∠APH=∠MAP,∠AFQ=∠BAF,
∵AF平分∠BAP,
∴∠BAF=∠PAF,
∴2∠AFQ=∠BAP,
∵PH∥AB,FQ∥AB,AB∥CD,
∴PH∥CD,FQ∥CD,
∴∠CPH=∠NCP,∠CFQ=∠DCF,
∵CF平分∠DCP,
∴∠DCF=∠PCF,
∴2∠CFQ=∠DCP,
∵∠BAP+∠MAP=180°,∠DCP+∠NCP=180°,
∴2∠AFQ+∠APH=180°,2∠CFQ+∠CPH=180°,
∴2∠AFQ+∠APH+2∠CFQ+∠CPH=360°,
即2∠AFC+∠APC=360°,
∴∠AFC=180°-![]() ∠APC,
∠APC,
故答案為:∠AFC=180°-![]() ∠APC.
∠APC.


科目:初中數學 來源: 題型:
【題目】已知,在平面直角坐標系中,點![]() 的坐標分別是
的坐標分別是![]() 且
且![]() .
.

(1)求![]() 的值;
的值;
(2)在![]() 軸上是否存在點
軸上是否存在點![]() ,使三角形
,使三角形![]() 的面積是
的面積是![]() ?若存在,求出點
?若存在,求出點![]() 的坐標;若不存在,請說明理由;
的坐標;若不存在,請說明理由;
(3)已知點![]() 是
是![]() 軸正半軸上一點,且到
軸正半軸上一點,且到![]() 軸的距離為
軸的距離為![]() ,若
,若![]() 點沿
點沿![]() 軸負半軸方向以每秒
軸負半軸方向以每秒![]() 個單位長度平移至點
個單位長度平移至點![]() ,當運動時間
,當運動時間![]() 為多少秒時,四邊形
為多少秒時,四邊形![]() 的面積
的面積![]() 為
為![]() 個平方單位?并寫出此時點
個平方單位?并寫出此時點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】中學生帶手機上學的現象越來越受到社會的關注,為此,某記者隨機調查了某城區若干名學生家長對這種現象的態度(態度分為:A:無所謂;B:基本贊成;C:贊成;D:反對),并將調查結果繪制成頻數折線圖1和統計圖2(不完整)。請根據圖中提供的信息,解答下列問題:
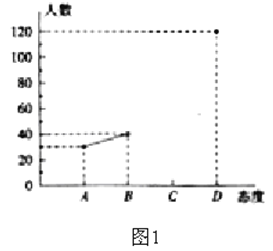
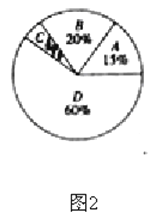
(1)此次抽樣檢查中,共調查了 名學生家長;
(2)將圖1補充完整;
(3)根據抽樣檢查的結果,請你估計該市城區6000名中學生家長中有多少名家長持反對態度?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠A=90°,∠C=30°,AD⊥BC于D,BE是∠ABC的平分線,且交AD于P,如果AP=2,則AC的長為( )
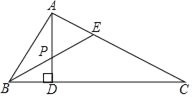
A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中數學 來源: 題型:
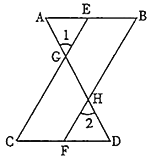
【題目】完成下面的證明:
如圖,已知![]() ,
,![]() ,可推得
,可推得![]() .
.
理由如下:∵![]() (已知),
(已知),
且![]() ( )
( )
∴![]() (等量代換)
(等量代換)
∴________∥________( )
∴∠________![]() ( )
( )
又∵![]() (已知)
(已知)
∴![]() ( )
( )
∴![]() ( )
( )
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(探究)如圖①,從邊長為a的大正方形中剪掉一個邊長為b的小正方形,有陰影部分沿虛線剪開,拼成圖②的長方形
(1)請你分別表示出這兩個圖形中陰影部分的面積
(2)比較兩圖的陰影部分面積,可以得到乘法公式 (用字母表示)
(應用)請應用這個公式完成下列各題
①已知![]() ,
,![]() ,則
,則![]() 的值為
的值為
②計算:![]()
(拓展)①![]() 結果的個位數字為
結果的個位數字為
②計算:![]()

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校開展了“讓世界充滿愛”的捐款助學活動,其中八(2)班全體同學的捐款情況如下表:
捐款金額(元) | 5 | 10 | 15 | 20 | 50 |
捐款人數(人) | 7 | 18 | 12 | 3 |
由于填表的同學不小心把墨水滴在了表上,致使表中數據不完整,但知道捐款金額為10元的人數為全班人數的36%,結合上表回答下列問題:
(1)八(2)班共有多少人?
(2)學生捐款金額的眾數和中位數分別為多少元?
(3)如果把該班學生的捐款情況繪制成扇形統計圖,則捐款金額為20元的人數所對應的扇形圓心角為多少度?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現規定:求若千個相同的有理數(均不等于![]() )的商的運算叫做除方,比如
)的商的運算叫做除方,比如![]() 等,類比有理數的乘方,我們把
等,類比有理數的乘方,我們把![]() 記作
記作![]() ,讀作“
,讀作“![]() 的圈
的圈![]() 次方”,
次方”,![]() 記作
記作![]() ,讀作“
,讀作“![]() 的圈
的圈![]() 次方”,一般地,把
次方”,一般地,把![]() 個
個![]()
![]() 相除記作
相除記作![]() ,讀作“
,讀作“![]() 的圈
的圈![]() 次方”.
次方”.
初步探究:(1)直接寫出結果:![]() .
.![]() .
.
(2)下列關于除方的說法中,錯誤的是
A.任何非零數的圈![]() 次方都等于
次方都等于![]()
B.對于任何正整數![]() 的圈
的圈![]() 次方等于
次方等于![]()
C.![]()
D.負數的圈奇數次方的結果是負數,負數的圈偶數次方的結果是正數
深入思考:我們知道,有理數的減法運算可以轉化為加法運算,除法運算可以轉化為乘法運算,有理數的除方運算如何轉化為乘方運算呢?
(3)試一試,把下列除方運算直接寫成冪的形式![]() .
. .
.
(4)想一想,請把有理數![]() 的圈
的圈![]() 次方寫成冪的形式.
次方寫成冪的形式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“重百”、“沃爾瑪”兩家超市出售同樣的保溫壺和水杯,保溫壺和水杯在兩家超市的售價分別一樣.已知買1個保溫壺和1個水杯要花費60元,買2個保溫壺和3個水杯要花費130元.
(1)請問:一個保溫壺與一個水杯售價各是多少元;(列方程組求解)
(2)為了迎接“五一勞動節”,兩家超市都在搞促銷活動,“重百”超市規定:這兩種商品都打九折;“沃爾瑪”超市規定:買一個保溫壺贈送一個水杯.若某單位想要買4個保溫壺和15個水杯,如果只能在一家超市購買,請問選擇哪家超市購買更合算,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com