
數學課上,李老師出示范了如下框中的題目.

小敏與同桌小聰討論后,進行了如下解答:
(1)特殊情況,探索結論
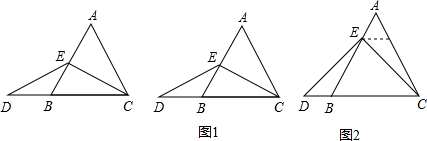
當點E為AB的中點時,如圖1,確定線段AE與DB的大小關系.請你直接寫出結論:AE DB(填“>”、“<”或“=”);
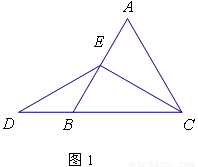
(2)特例啟發,解答題目
解:題目中,AE與DB的大小關系是:AE DB(填“>”、“<”或“=”).理由如下:
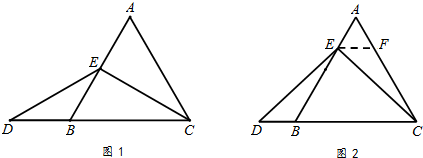
如圖2過點E作EF∥BC,交AC于點F;(請你完成以下解答過程)
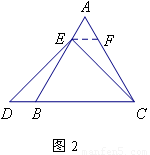
(3)拓展結論,設計新題
在等邊三角形ABC中,點E在直線AB上,點D在直線BC上,且ED=EC.若△ABC的邊長為1,AE=2,求CD的長(請你直接寫出結果).
(1)=;(2)=;(3)1或3
【解析】
試題分析:(1)根據等邊三角形的性質和三角形的內角和定理求出∠D=∠ECB=30°,∠ABC=60°,求出∠D=∠DEB=30°,推出DB=BE=AE即可得到答案;
(2)作EF∥BC,證出等邊三角形AEF,再證△DBE≌△EFC即可得到答案;
(3)分為四種情況:畫出圖形,根據等邊三角形性質求出符合條件的CD即可.
(1)答案為:AE=DB;
(2)答案為:AE=DB
證明:在等邊△ABC中,∠ABC=∠ACB=∠BAC=60°,AB=BC=AC,
∵EF∥BC,
∴∠AEF=∠ABC,∠AFE=∠ACB,
∴∠AEF=∠AFE=∠BAC=60°,
∴AE=AF=EF,
∴AB-AE=AC-AF,
即BE=CF,
∵∠ABC=∠EDB+∠BED,∠ACB=∠ECB+∠FCE,
∵ED=EC,
∴∠EDB=∠ECB,
∵∠EBC=∠EDB+∠BED,∠ACB=∠ECB+∠FCE,
∴∠BED=∠FCE,
∴△DBE≌△EFC(SAS),
∴DB=EF,
∴AE=BD.
(3)分為四種情況:
如圖1:
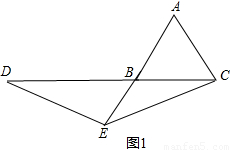
∵AB=AC=1,AE=2,
∴B是AE的中點,
∵△ABC是等邊三角形,
∴AB=AC=BC=1,△ACE是直角三角形(根據直角三角斜邊的中線等于斜邊的一半),
∴∠ACE=90°,∠AEC=30°,
∴∠D=∠ECB=∠BEC=30°,∠DBE=∠ABC=60°,
∴∠DEB=180°-30°-60°=90°,
即△DEB是直角三角形.
∴BD=2BE=2(30°所對的直角邊等于斜邊的一半),
即CD=1+2=3.
如圖2,
過A作AN⊥BC于N,過E作EM⊥CD于M,
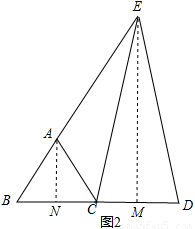
∵等邊三角形ABC,EC=ED,
∴BN=CN=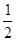 BC=
BC=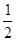 ,CM=MD=
,CM=MD=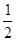 CD,AN∥EM,
CD,AN∥EM,
∴△BAN∽△BEM,
∴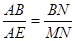 ,
,
∵△ABC邊長是1,AE=2,
∴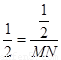 ,解得
,解得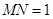
∴CM=MN-CN=1-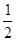 =
=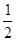 ,
,
∴CD=2CM=1;
如圖3,
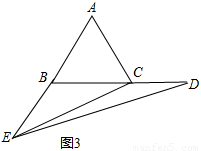
∵∠ECD>∠EBC(∠EBC=120°),而∠ECD不能等于120°,否則△EDC不符合三角形內角和定理,
∴此時不存在EC=ED;
如圖4
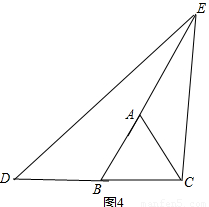
∵∠EDC<∠ABC,∠ECB>∠ACB,
又∵∠ABC=∠ACB=60°,
∴∠ECD>∠EDC,
即此時ED≠EC,
∴此時情況不存在,
答:CD的長是3或1.
考點:全等三角形的性質和判定,三角形的內角和定理,等邊三角形的性質和判定
點評:本題綜合性較強,難度較大,是中考常見題,綜合運用考點中的性質進行推理是解此題的關鍵.


科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:
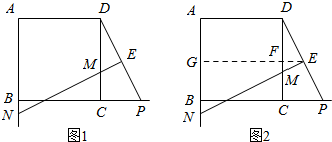
| DF |
| FC |
| DE |
| EP |
查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com