
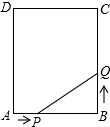
 如圖,矩形ABCD中,AB=6cm,BC=12cm,點P從A開始沿AB邊向點B以1厘米/秒的速度移動,點Q從點B開始沿BC邊向點C以2厘米/秒的速度移動.如果P、Q分別是從A、B同時出發,
如圖,矩形ABCD中,AB=6cm,BC=12cm,點P從A開始沿AB邊向點B以1厘米/秒的速度移動,點Q從點B開始沿BC邊向點C以2厘米/秒的速度移動.如果P、Q分別是從A、B同時出發,分析 (1)設xs后,△PBQ的面積等于9cm2,根據${S_{△PBQ}}=\frac{1}{2}PB•BQ$,列方程求解可得;
(2)由PB2+BQ2=PQ2得(6-x)2+(2x)2=52,即可判斷;
(3)由S五邊形APQCD=S矩形ABCD-S△PBQ=AB•BC-$\frac{1}{2}$PB•BQ=72-6x+x2=(x-3)2+63,即可得答案.
解答 解:(1)設xs后,△PBQ的面積等于9cm2,
此時,AP=xcm,PB=(6-x)cm,BQ=2xcm.
由${S_{△PBQ}}=\frac{1}{2}PB•BQ$,得 $9=\frac{1}{2}(6-x)•2x$.
解得 x1=x2=3.
答:3秒后,△PBQ的面積等于9平方厘米;
(2)點P與點Q之間的距離不可能為5厘米.
由PB2+BQ2=PQ2得(6-x)2+(2x)2=52,
整理,得 5x2-12x+11=0,
容易判斷此方程無實數根.
答:點P與點Q之間的距離不可能為5厘米;
(3)由S五邊形APQCD=S矩形ABCD-S△PBQ
=AB•BC-$\frac{1}{2}$PB•BQ
=6×12-$\frac{1}{2}$×(6-x)•2x
=72-6x+x2
=(x-3)2+63,
∵(x-3)2≥0,
∴當x-3=0時,即(x-3)2的值為0時是最小值,
∴當x=3時,(x-3)2+63有最小值,此時為63.
答:3秒后,五邊形APQCD的面積最小,最小值是63cm2.
點評 本題主要考查二次函數的應用,根據三角形的面積、勾股定理、五邊形的面積列出方程或函數解析式是解題的關鍵.


 提分百分百檢測卷單元期末測試卷系列答案
提分百分百檢測卷單元期末測試卷系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
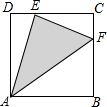 如圖,正方形ABCD的邊長為10,E是邊DC上一點,F是邊BC上一點,且DE=CF.問:當點E在什么位置時,△AEF的面積最小?最小面積是多少?
如圖,正方形ABCD的邊長為10,E是邊DC上一點,F是邊BC上一點,且DE=CF.問:當點E在什么位置時,△AEF的面積最小?最小面積是多少?查看答案和解析>>
科目:初中數學 來源: 題型:解答題
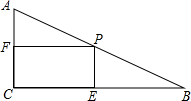 如圖,在Rt△ABC中,∠C=90°,∠B=30°,AB=12cm,動點P從點B開始沿邊BA以2cm/s的速度向點A移動,過點P作PE⊥BC,PF⊥AC,設點P移動的時間為t,四邊形PECF的面積為S.
如圖,在Rt△ABC中,∠C=90°,∠B=30°,AB=12cm,動點P從點B開始沿邊BA以2cm/s的速度向點A移動,過點P作PE⊥BC,PF⊥AC,設點P移動的時間為t,四邊形PECF的面積為S.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
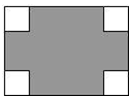 如圖,在長為10cm,寬為8cm的矩形的四個角上截去四個全等的小正方形,使得留下的圖形(圖中陰影部分)面積是原矩形面積的80%,則所截去小正方形的邊長是2cm.
如圖,在長為10cm,寬為8cm的矩形的四個角上截去四個全等的小正方形,使得留下的圖形(圖中陰影部分)面積是原矩形面積的80%,則所截去小正方形的邊長是2cm.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com