
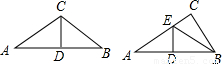
 解:(1)當AB為底邊時:∵∠CAD=50°,
解:(1)當AB為底邊時:∵∠CAD=50°,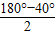 =70°;
=70°;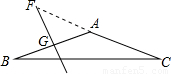
 ∠FAG=20°.
∠FAG=20°.

科目:初中數學 來源: 題型:
 24、等腰△ABC中,AB=AC,D為BC上的一動點,DE∥AC,DF∥AB,分別交AB于E,AC于F,則DE+DF是否隨D點變化而變化?請說明理由.
24、等腰△ABC中,AB=AC,D為BC上的一動點,DE∥AC,DF∥AB,分別交AB于E,AC于F,則DE+DF是否隨D點變化而變化?請說明理由.查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,在等腰△ABC中,AB=AC,以AB為直徑作⊙O交BC于D,交AC于E,過D點作DF⊥AC于F,有下列結論:
如圖,在等腰△ABC中,AB=AC,以AB為直徑作⊙O交BC于D,交AC于E,過D點作DF⊥AC于F,有下列結論:查看答案和解析>>
科目:初中數學 來源: 題型:
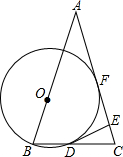 如圖,在等腰△ABC中,AB=AC,O為AB上一點,以O為圓心,OB長為半徑的圓交BC于D,DE⊥AC交AC于點E.
如圖,在等腰△ABC中,AB=AC,O為AB上一點,以O為圓心,OB長為半徑的圓交BC于D,DE⊥AC交AC于點E.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com