
【題目】如圖,在矩形 OABC中,OA=3,OC=5,分別以 OA、OC所在直線為x 軸、y 軸,建立平面直角坐標系,D是邊CB上的一個動點(不與C、B重合),反比例函數y=![]() (k>0)的圖象經過點D且與邊BA交于點E,連接DE.
(k>0)的圖象經過點D且與邊BA交于點E,連接DE.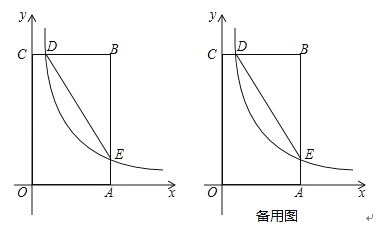
(1)連接OE,若△EOA的面積為2,則k=
(2)連接CA,DE與CA是否平行?請說明理由:
(3)是否存在點D,使得點B關于DE的對稱點在OC上?若存在,求出點D的坐標;若不存在,請說明理由:
【答案】
(1)4
(2)
解:連接AC,如圖1,
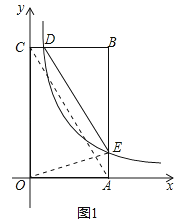
設D(x,5),E(3,![]() ),則BD=3﹣x,BE=5﹣
),則BD=3﹣x,BE=5﹣![]() ,
,![]() =
=![]() ,
,![]() =
=![]() ,∴
,∴![]() =
=![]() ∴DE∥AC.
∴DE∥AC.
(3)
解:假設存在點D滿足條件.設D(x,5),E(3,![]() ),則CD=x,BD=3﹣x,BE=5﹣
),則CD=x,BD=3﹣x,BE=5﹣![]() ,AE=
,AE=![]() .作EF⊥OC,垂足為F,如圖2,
.作EF⊥OC,垂足為F,如圖2,
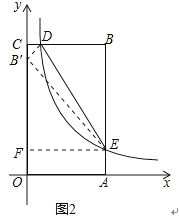
易證△B′CD∽△EFB′,∴![]() ,即
,即![]() =
=![]() ,∴B′F=
,∴B′F=![]() ,∴OB′=B′F+OF=B′F+AE=
,∴OB′=B′F+OF=B′F+AE=![]() +
+![]() =
=![]() ,
,
∴CB′=OC﹣OB′=5﹣![]() ,在Rt△B′CD中,CB′=5﹣
,在Rt△B′CD中,CB′=5﹣![]() ,CD=x,B′D=BD=3﹣x,由勾股定理得,CB′2+CD2=B′D2,
,CD=x,B′D=BD=3﹣x,由勾股定理得,CB′2+CD2=B′D2,
(5﹣![]() )2+x2=(3﹣x)2,解這個方程得,x1=1.5(舍去),x2=0.96,∴滿足條件的點D存在,D的坐標為D(0.96,5).
)2+x2=(3﹣x)2,解這個方程得,x1=1.5(舍去),x2=0.96,∴滿足條件的點D存在,D的坐標為D(0.96,5).
【解析】(1)連接OE,如,圖1,∵Rt△AOE的面積為2,∴k=2×2=4.
(1)連接OE,根據反比例函數k的幾何意義,即可求出k的值;(2)連接AC,設D(x,5),E(3,![]() ),則BD=3﹣x,BE=5﹣
),則BD=3﹣x,BE=5﹣![]() ,得到
,得到![]() =
=![]() ,從而求出DE∥AC.(3)假設存在點D滿足條件.設D(x,5),E(3,
,從而求出DE∥AC.(3)假設存在點D滿足條件.設D(x,5),E(3,![]() ),則CD=x,BD=3﹣x,BE=5﹣
),則CD=x,BD=3﹣x,BE=5﹣![]() ,AE=
,AE=![]() .作EF⊥OC,垂足為F,易得,△B′CD∽△EFB′,然后根據對稱性求出B′E、B′D的表達式,列出
.作EF⊥OC,垂足為F,易得,△B′CD∽△EFB′,然后根據對稱性求出B′E、B′D的表達式,列出![]() , 即
, 即![]() =
=![]() , , 從而求出(5﹣
, , 從而求出(5﹣![]() )2+x2=(3﹣x)2 , 即可求出x值,從而得到D點坐標.
)2+x2=(3﹣x)2 , 即可求出x值,從而得到D點坐標.


 陽光試卷單元測試卷系列答案
陽光試卷單元測試卷系列答案科目:初中數學 來源: 題型:
【題目】某校申報“跳繩特色運動”學校一年后,抽樣調查了部分學生的“1分鐘跳繩”成績,并制成了下面的頻數分布直方圖(每小組含最小值,不含最大值)和扇形圖.
(1)補全頻數分布直方圖,扇形圖中m= ;
(2)若把每組中各個數據用這組數據的中間值代替(如A組80≤x<100的中間值是![]() =90次),則這次調查的樣本平均數是多少?
=90次),則這次調查的樣本平均數是多少?
(3)如果“1分鐘跳繩”成績大于或等于120次為優秀,那么該校2100名學生中“1分鐘跳繩”成績為優秀的大約有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,若銳角△ABC內接于⊙O,點D在⊙O外(與點C在AB同側),則下列三個結論:①sin∠C>sin∠D;②cos∠C>cos∠D;③tan∠C>tan∠D中,正確的結論為( )
A.①②
B.②③
C.①②③
D.①③
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,一幢樓房AB背后有一臺階CD,臺階每層高0.2米,且AC=17.2米,設太陽光線與水平地面的夾角為α,當α=60°時,測得樓房在地面上的影長AE=10米,現有一只小貓睡在臺階的MN這層上曬太陽.(![]() 取1.73)
取1.73)
(1)求樓房的高度約為多少米?
(2)過了一會兒,當α=45°時,問小貓能否還曬到太陽?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明參加某網店的“翻牌抽獎”活動,如圖,4張牌分別對應價值5,10,15,20(單位:元)的4件獎品.
(1)如果隨機翻1張牌,那么抽中20元獎品的概率為
(2)如果隨機翻2張牌,且第一次翻過的牌不再參加下次翻牌,則所獲獎品總值不低于30元的概率為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:⊙O上兩個定點A,B和兩個動點C,D,AC與BD交于點E.
(1)如圖1,求證:EAEC=EBED
(2)如圖2,若![]() , AD是⊙O的直徑,求證:ADAC=2BDBC
, AD是⊙O的直徑,求證:ADAC=2BDBC
(3)如圖3,若AC⊥BD,點O到AD的距離為2,求BC的長
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=x2+mx+n的圖象經過點P(﹣3,1),對稱軸是經過(﹣1,0)且平行于y軸的直線.
(1)求m、n的值
(2)如圖,一次函數y=kx+b的圖象經過點P,與x軸相交于點A,與二次函數的圖象相交于另一點B,點B在點P的右側,PA:PB=1:5,求一次函數的表達式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com