
【題目】如圖,在三角形![]() 中,
中,![]() ,垂足為點
,垂足為點![]() ,直線
,直線![]() 過點
過點![]() ,且
,且![]() ,點
,點![]() 為線段
為線段![]() 上一點,連接
上一點,連接![]() ,∠BCG與∠BCE的角平分線CM、CN分別交
,∠BCG與∠BCE的角平分線CM、CN分別交![]() 于點M、N,若
于點M、N,若![]() ,則
,則![]() =_________°.
=_________°.

【答案】![]()
【解析】
依據![]() 得90°-∠B=∠BAD,已知90°-∠FCB=∠BAD,可得∠FCB=∠B,進而判定EF∥AB,即可得到∠ECG=∠BGC=70°,再根據∠MCN=∠BCN-∠BCM=
得90°-∠B=∠BAD,已知90°-∠FCB=∠BAD,可得∠FCB=∠B,進而判定EF∥AB,即可得到∠ECG=∠BGC=70°,再根據∠MCN=∠BCN-∠BCM=![]() (∠BCE-∠BCG)=
(∠BCE-∠BCG)=![]() ∠ECG,即可得到結論.
∠ECG,即可得到結論.
解:∵AD⊥BC,
∴Rt△ABD中,90°-∠B=∠BAD,
又∵90°-∠FCB=∠BAD,
∴∠FCB=∠B,
∴EF∥AB,
∴∠ECG=∠BGC=70°,
∵∠BCG與∠BCE的角平分線CM、CN分別交AD于點M、N,
∴∠BCN=![]() ∠BCE,∠BCM=
∠BCE,∠BCM=![]() ∠BCG,
∠BCG,
∴∠MCN=∠BCN-∠BCM=![]() (∠BCE-∠BCG)=
(∠BCE-∠BCG)=![]() ∠ECG,
∠ECG,
∵∠ECG=∠BGC=70°,
∴∠MCN=![]() ×70°=35°,
×70°=35°,
故答案為:35.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,AE⊥BD,CF⊥BD,E,F分別為垂足.
(1)求證:四邊形AECF是平行四邊形;
(2)如果AE=3,EF=4,求AF、EC所在直線的距離.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)解方程:![]()
(2)計算:3a(2a2-9a+3)-4a(2a-1)
(3)計算:(![]() )×(
)×(![]() )+|
)+|![]() -1|+(5-2π)0
-1|+(5-2π)0
(4)先化簡,再求值:(xy2+x2y)![]() ,其中x=
,其中x=![]() ,y=
,y=![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1所示,從邊長為a的正方形紙片中減去一個邊長為b的小正方形,再沿著線段AB剪開,把剪成的兩張紙拼成如圖2的等腰梯形(其面積= ![]() ).
).
(1)設圖1中陰影部分面積為S1,圖2中陰影部分面積為S2,請直接用含a、b的式子表示S1和S2;
(2)請寫出上述過程所揭示的乘法公式.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB⊥BC于點B,DC⊥BC于點C,DE平分∠ADC交BC于點E,點F為線段CD延長線上一點,∠BAF=∠EDF.
(1)求證:∠DAF=∠F;
(2)在不添加任何輔助線的情況下,請直接寫出所有與∠CED互余的角.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標中,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的坐標為
的坐標為![]() ,將線段
,將線段![]() 向右平移
向右平移![]() 個單位長度得到線段
個單位長度得到線段![]() (點
(點![]() 和點
和點![]() 分別是點
分別是點![]() 和點
和點![]() 的對應點),連接
的對應點),連接![]() 、
、![]() ,點
,點![]() 是線段
是線段![]() 的中點.
的中點.

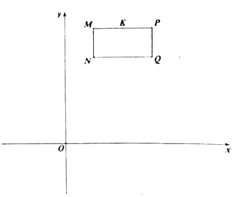
備用圖
(1)求點![]() 的坐標;
的坐標;
(2)若長方形![]() 以每秒
以每秒![]() 個單位長度的速度向正下方運動,(點
個單位長度的速度向正下方運動,(點![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 分別是點
分別是點![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 的對應點),當
的對應點),當![]() 與
與![]() 軸重合時停止運動,連接
軸重合時停止運動,連接![]() 、
、![]() ,設運動時間為
,設運動時間為![]() 妙,請用含
妙,請用含![]() 的式子表示三角形
的式子表示三角形![]() 的面積
的面積![]() (不要求寫出
(不要求寫出![]() 的取值范圍);
的取值范圍);
(3)在(2)的條件下,連接![]() 、
、![]() ,問是否存在某一時刻
,問是否存在某一時刻![]() ,使三角形
,使三角形![]() 的面積等于三角形
的面積等于三角形![]() 的面積?若存在,請求出
的面積?若存在,請求出![]() 值;若不存在,請說明理由.
值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,⊙O的半徑為1,P是坐標系內任意一點,點P到⊙O的距離SP的定義如下:若點P與圓心O重合,則SP為⊙O的半徑長;若點P與圓心O不重合,作射線OP交⊙O于點A,則SP為線段AP的長度.
圖1為點P在⊙O外的情形示意圖.
(1)若點B(1,0),C(1,1),D(0, ![]() ),則SB=;SC=;SD=;
),則SB=;SC=;SD=;
(2)若直線y=x+b上存在點M,使得SM=2,求b的取值范圍;
(3)已知點P,Q在x軸上,R為線段PQ上任意一點.若線段PQ上存在一點T,滿足T在⊙O內且ST≥SR , 直接寫出滿足條件的線段PQ長度的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,一次函數y=﹣2x的圖象與反比例函數y= ![]() 的圖象交于點A(﹣1,n).
的圖象交于點A(﹣1,n).
(1)求反比例函數y= ![]() 的解析式;
的解析式;
(2)若P是坐標軸上一點,且滿足PA=OA,直接寫出點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀:已知a+b=﹣4,ab=3,求a2+b2的值.
解:∵a+b=﹣4,ab=3,
∴a2+b2=(a+b)2﹣2ab=(﹣4)2﹣2×3=10.
請你根據上述解題思路解答下面問題:
(1)已知a﹣b=﹣3,ab=﹣2,求(a+b)(a2﹣b2)的值.
(2)已知a﹣c﹣b=﹣10,(a﹣b)c=﹣12,求(a﹣b)2+c2的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com