
【題目】某市政府2007年準備投入一定資金加大對主城區的改造力度,但又不影響對教育及其他方面的投入.下面是市規劃局等部門提供的信息:
2002年 | 2003年 | 2004年 | 2005年 | |
政府劃撥資金 | 1.2 | 1.4 | 1.5 | 1.6 |
招商引進資金 | 5.8 | 6.1 | 6.25 | 6.4 |
①2007年用于主城區改造的資金不超過2007年教育投入的3倍.
②計劃2007年比2006年的教育投入多0.5億元,這樣兩年的教育投入之比為6:5.
③用于主城區改造的資金一部分由政府劃撥,其余來源于招商引資.據分析發現,招商所引資金與政府劃撥的資金始終滿足某種函數關系.(如下表所示)
政府劃撥資金與招商引進資金對照表:(單位:億元)
④2007年招商引資的投資者從2008年起每年共可獲得0.67億元的回報,估計2007年招商引進的資金至少10年方可收回.
(1)該市政府2006年對教育的投入為多少億元?
(2)求招商引進資金y(單位:億元)與財政劃撥部分x(單位:億元)之間的函數關系式;
(3)求2007年該市在主城區改造中財政劃撥的資金的范圍.
【答案】(1)該市政府2006年對教育的投入為2.5億元;(2)y=1.5x+4;(3)2007年該市在主城區改造中財政劃撥的資金在1.8億元﹣2億元之間(包括1.8億元,2億元).
【解析】
(1)設該市政府2006年對教育的投入為a億元,利用信息②列出方程,解方程即可;(2)將x,y的四組對應值分別作為橫縱坐標在同一平面直角坐標系中描出4個對應點.
猜想y是x的一次函數.設y=kx+b,代入數據解出函數,然后進行驗證即可;(3)根據題意列出不等式組解不等式組即可
解:(1)設該市政府2006年對教育的投入為a億元,
依題意可得:![]()
解之得:a=2.5,
答:該市政府2006年對教育的投入為2.5億元.
(2)將x,y的四組對應值分別作為橫縱坐標在同一平面直角坐標系中描出4個對應點.
猜想y是x的一次函數.
設y=kx+b,
將其中的兩組對應值代入求得k=1.5,b=4,
將另外兩組對應值代入驗證適合,故y=1.5x+4;
(3)依題意可得:![]()
解得:1.8≤x≤2.
答:2007年該市在主城區改造中財政劃撥的資金在1.8億元﹣﹣2億元之間(包括1.8億元,2億元).


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
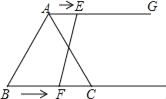
【題目】如圖,在等邊三角形ABC中,BC=6cm,射線AG∥BC,點E從點A出發沿射線AG以1cm/s的速度運動,點F從點B出發沿射線BC以2cm/s的速度運動.如果點E、F同時出發,設運動時間為t(s)當t=______s時,以A、C、E、F為頂點四邊形是平行四邊形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)解方程組或不等式組
①解方程組
②解不等式組 把解集在數軸上表示出來,并寫出不等式組的負整數解.
把解集在數軸上表示出來,并寫出不等式組的負整數解.
(2)甲、乙兩位同學一起解方程組 ,由于甲看錯了方程①中的
,由于甲看錯了方程①中的![]() ,得到的解為
,得到的解為![]() ,乙看錯了方程②中的
,乙看錯了方程②中的![]() ,得到的解為
,得到的解為![]() ,試計算的
,試計算的![]() 值.
值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】阿左旗教育局準備舉辦一場“中國漢字聽寫大賽”,要求每校推選一名同學參加比賽,為此某學校組織了五輪選拔賽,在這五輪選拔賽中,甲同學的得分是:8、7、9、8、8,乙同學的得分是:7、9、6、9、9則下列說法中錯誤的是( )
A.甲乙得分的平均數都是8B.甲得分的眾數是8,乙得分的眾數9
C.甲得分的方差比乙得分的方差小D.甲得分的中位數是9,乙得分的中位數是6
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的一元二次方程x2﹣2x+m﹣1=0有兩個實數根.
(1)求m的取值范圍;
(2)設p是方程的一個實數根,且滿足(p2﹣2p+3)(m+4)=7,求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某教研機構為了解在校初中生閱讀數學教科書的現狀,隨機抽取某校部分初中學生進行了調查.依據相關數據繪制成如圖所示的不完整的統計圖表,請根據圖表中的信息解答下列問題:
某校初中生閱讀數學教科書情況統計圖表

類別 | 人數 | 占總人數比例 |
重視 | a | 0.3 |
一般 | 57 | 0.38 |
不重視 | b | c |
說不清楚 | 9 | 0.06 |
(1)求樣本容量及表格中a,b,c的值,并補全統計圖.
(2)若該校共有初中生2 300名,請估計該校“不重視閱讀數學教科書”的初中生人數.
(3)①根據上面的統計結果,談談你對該校初中生閱讀數學教科書的現狀的看法及建議;
②如果要了解全省初中生閱讀數學教科書的情況,你認為應該如何進行抽樣?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形OABC中,A(6,0)、C(0,2![]() )、D(0,3
)、D(0,3![]() ),射線l過點D且與x軸平行,點P、Q分別是l和x軸正半軸上動點,滿足∠PQO=60°.
),射線l過點D且與x軸平行,點P、Q分別是l和x軸正半軸上動點,滿足∠PQO=60°.
(1)①點B的坐標是 ;②∠CAO= 度;③當點Q與點A重合 時,點P的坐標為 ;(直接寫出答案)
(2)設OA的中點為N,PQ與線段AC相交于點M,是否存在點P,使△AMN為等腰三角形?若存在,請直接寫出點P的橫坐標為m;若不存在,請說明理由.
(3)設點P的橫坐標為x,△OPQ與矩形OABC的重疊部分的面積為S,試求S與x的函數關系式和相應的自變量x的取值范圍.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在⊙O中,點C在劣弧![]() 上,D是弦AB上的點,∠ACD=40°.
上,D是弦AB上的點,∠ACD=40°.
(1)如圖1,若⊙O的半徑為3,∠CDB=70°,求![]() 的長;
的長;
(2)如圖2,若DC的延長線上存在點P,使得PD=PB,試探究∠ABC與∠OBP的數量關系,并加以證明.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com