
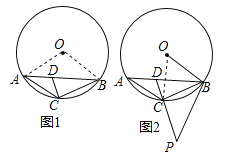
【題目】在⊙O中,點C在劣弧![]() 上,D是弦AB上的點,∠ACD=40°.
上,D是弦AB上的點,∠ACD=40°.
(1)如圖1,若⊙O的半徑為3,∠CDB=70°,求![]() 的長;
的長;
(2)如圖2,若DC的延長線上存在點P,使得PD=PB,試探究∠ABC與∠OBP的數量關系,并加以證明.

【答案】(1)π;(2)∠ABC+∠OBP=130°.
【解析】試題分析:
試題解析:
(1)如圖1,連接OC,OB.
∵∠ACD=40°,∠CDB=70°
∴∠CAB=∠CDB﹣∠ACD=70°﹣40°=30°,
∴∠BOC=2∠BAC=60°,
∴弧BD=![]() =
=![]() =π.
=π.
(2)∠ABC+∠OBP=130°,
證明:設∠CAB=α,∠ABC=β,∠OBA=γ,
如圖2,連接OC,則∠COB=2α,∵OB=OC,
∴∠OCB=∠OBC=β+γ,
∵△OCB中,∠COB+∠OCB+∠OBC=180°,
∴2α+2(β+γ)=180°,即α+β+γ=90°,
∵PB=PD,
∴∠PBD=∠PDB=40°+α,
∴∠OBP=∠OBA+∠PBD
=γ+40°+α
=(90°﹣β)+40°
=130°﹣β,即∠ABC+∠OBP=130°.


科目:初中數學 來源: 題型:
【題目】某市政府2007年準備投入一定資金加大對主城區的改造力度,但又不影響對教育及其他方面的投入.下面是市規劃局等部門提供的信息:
2002年 | 2003年 | 2004年 | 2005年 | |
政府劃撥資金 | 1.2 | 1.4 | 1.5 | 1.6 |
招商引進資金 | 5.8 | 6.1 | 6.25 | 6.4 |
①2007年用于主城區改造的資金不超過2007年教育投入的3倍.
②計劃2007年比2006年的教育投入多0.5億元,這樣兩年的教育投入之比為6:5.
③用于主城區改造的資金一部分由政府劃撥,其余來源于招商引資.據分析發現,招商所引資金與政府劃撥的資金始終滿足某種函數關系.(如下表所示)
政府劃撥資金與招商引進資金對照表:(單位:億元)
④2007年招商引資的投資者從2008年起每年共可獲得0.67億元的回報,估計2007年招商引進的資金至少10年方可收回.
(1)該市政府2006年對教育的投入為多少億元?
(2)求招商引進資金y(單位:億元)與財政劃撥部分x(單位:億元)之間的函數關系式;
(3)求2007年該市在主城區改造中財政劃撥的資金的范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
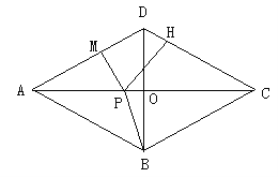
【題目】(13分)如圖所示,四邊形![]() 中,
中, ![]() 于點
于點![]() ,
, ![]() ,
, ![]() ,點
,點![]() 為線段
為線段![]() 上的一個動點。
上的一個動點。
(1)求證: ![]() 。
。
(2)過點![]() 分別作
分別作![]() 于
于![]() 點,作
點,作![]() 于
于![]() 點。
點。
① 試說明![]() 為定值。
為定值。
② 連結![]() ,試探索:在點
,試探索:在點![]() 運動過程中,是否存在點
運動過程中,是否存在點![]() ,使
,使![]() 的值最小。若存在,請求出該最小值;若不存在,請說明理由。
的值最小。若存在,請求出該最小值;若不存在,請說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
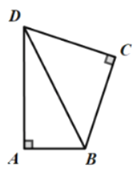
【題目】在四邊形![]() 中,
中,![]() .
.
(1)如圖,若![]() ,
,![]() ,
,![]() ,求
,求![]() 的長;
的長;
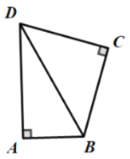
(2)如圖,若![]() ,連接
,連接![]() ,求證:
,求證:![]() 平分
平分![]() ;
;
(3)在(2)的條件下,若![]() ,
,![]() ,直接寫出
,直接寫出![]() 的長度為________.
的長度為________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了從甲、乙兩名選手中選拔一個參加射擊比賽,現對他們進行一次測驗,兩個人在相同條件下各射靶![]() 次,為了比較兩人的成績,制作了如下統計圖表:
次,為了比較兩人的成績,制作了如下統計圖表:
甲乙射擊成績統計表
平均數 | 中位數 | 方差 | 命中 | |
甲 |
|
| ||
乙 |
|
|
|
甲乙射擊成績折線圖
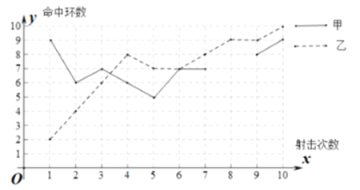
(1)請補全上述圖表(請直接在統計表中填空和補全折線圖);
(2)如果規定成績較穩定者勝出,則_____勝出,理由是____________________;
(3)如果希望(2)中的另一名選手勝出,根據圖表中的信息,應該制定怎樣的評判規則?說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】平價大藥房準備購進![]() 、一次性醫用兩種口罩.兩種口罩的進價和售價如表.已知:用
、一次性醫用兩種口罩.兩種口罩的進價和售價如表.已知:用![]() 元購進一次性醫用口罩的數量是用
元購進一次性醫用口罩的數量是用![]() 元購進
元購進![]() 口罩的數量的
口罩的數量的![]() 倍.
倍.
| 一次性醫用口罩 | |
進價(元 |
|
|
售價(元 |
|
|
(1)求![]() 的值;
的值;
(2)要使購進的![]() 、一次性醫用兩種口罩共
、一次性醫用兩種口罩共![]() 個的總利潤不少于
個的總利潤不少于![]() 元,且不超過
元,且不超過![]() 元,問該藥店共有多少種進貨方案?
元,問該藥店共有多少種進貨方案?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】威麗商場銷售A、B兩種商品,售出1件A種商品和4件B種商品所得利潤為600元;售出3件A種商品和5件B種商品所得利潤為1100元.
(1)求每件A種商品和每件B種商品售出后所得利潤分別為多少元?
(2)由于需求量大,A、B兩種商品很快售完,威麗商場決定再一次購進A、B兩種商品共34件,如果將這34件商品全部售完后所得利潤不低于4000元,那么威麗商場至少需購進多少件A種商品?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一個不透明的口袋中,放有三個標號分別為1,2,3的質地、大小都相同的小球.任意摸出一個小球,記為x,再從剩余的球中任意摸出一個小球,又記為y,得到點(x,y).
(1)用畫樹狀圖或列表等方法求出點(x,y)的所有可能情況;
(2)求點(x,y)在二次函數y=ax2﹣4ax+c(a≠0)圖象的對稱軸上的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】光明電器超市銷售每臺進價分別為190元、160元的A、B兩種型號的電風扇,下表是近兩周的銷售情況:
銷售時段 | 銷售數量 | 銷售收入 | |
A種型號 | B種型號 | ||
第一周 | 2臺 | 6臺 | 1840元 |
第二周 | 5臺 | 7臺 | 2840 元 |
(進價、售價均保持不變,利潤=銷售收入-進貨成本)
(1)求A、B兩種型號的電風扇的銷售單價;
(2)若超市準備再采購這兩種型號的電風扇共40臺,這40臺電風扇全部售出后,若利潤不低于2660元,求A種型號的電風扇至少要采購多少臺?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com