(本題10分)
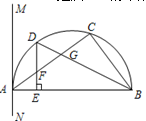
如圖,△
ABC內(nèi)接于半圓,
AB是直徑,過
A作直線
MN,∠
MAC=∠
ABC,
D是弧
AC的中點,連接
BD交
AC于
G,過
D作
DE⊥
AB于
E,交
AC于
F.
(1)求證:
MN是半圓的切線;
(2)求證:
FD=FG;
(3)若△
DFG的面積為4.5,且
DG=3,
GC=4,試求△
BCG的面積.
(1)證明:
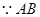
是直徑,
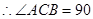
°即
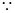
∠
MAC=∠
ABC,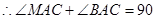 °,即
°,即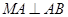
所以
MN是半圓的切線;
(2) ∵D是弧AC的中點,∴∠DBC=∠2
∵AB是直徑,∴∠CBG+∠CGB=90º
∵DE⊥AB,∴∠FDG+∠2=90º
∵∠DBC=∠2,∴∠FDG=∠CGB=∠FGD
∴FD=F∵∠ADB=90º,DE⊥AB,∴∠3=∠2
∵∠1=∠2,∴∠1=∠3
∴AF=DF=FG
(3)∵∠ADG=∠BCG,∠DGA=∠CGB
∴△ADG∽△BCG
∴
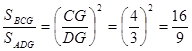
∴S△BCG=

此題考查切線的判定、圓的有關(guān)知識、三角形的面積。
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:初中數(shù)學(xué)
來源:不詳
題型:填空題
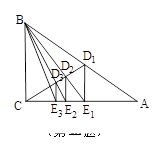
如圖,已知Rt△ABC,D
1是斜邊AB的中點,過D
1作D
1E
1⊥AC于E
1,連結(jié)BE
1交CD
1于D
2;過D
2作D
2E
2⊥AC于E
2,連結(jié)BE
2交CD
1于D
3;過D
3作D
3E
3⊥AC于E
3,…,如此繼續(xù),可以依次得到點E
4、E
5、…、E
n,分別記△BCE
1、△BCE
2、△BCE
3···△BCE
n的面積為S
1、S
2、S
3、…S
n. 則S
n=
▲ S
△ABC(用含n的代數(shù)式表示).
查看答案和解析>>
科目:初中數(shù)學(xué)
來源:不詳
題型:解答題
如圖,在正方形
ABCD中,
E為對角線
AC上一點,聯(lián)結(jié)
EB、
ED,延長
BE交
AD于點
F.

(1)求證:∠
BEC =∠
DEC ;
(2)當(dāng)
CE=
CD時,求證:
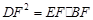
.
查看答案和解析>>
科目:初中數(shù)學(xué)
來源:不詳
題型:解答題
如圖所示,已知:⊿ABC∽⊿DAC,AD=2,AC=4,BC=6,∠B=36°,∠D=117°,

(1)求AB的長;
(2)求CD的長;
(3)求∠BAD的大小。
查看答案和解析>>
科目:初中數(shù)學(xué)
來源:不詳
題型:解答題
(12分)如圖1,在平面上,給定了半徑為
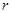
的⊙

,對于任意點
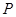
,在射線

上取一點

,使得

·
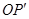
=
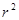
,這種把點
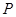
變?yōu)辄c

的變換叫做反演變換,點
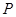
與點

叫做互為反演點,⊙

稱為基圓.
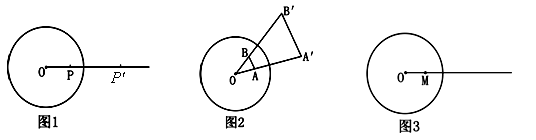
⑴如圖2,⊙

內(nèi)有不同的兩點
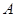
、
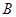
,它們的反演點分別是
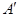
、
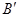
,則與∠
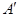
一定相等的角是( ▲ )
⑵如圖3,⊙

內(nèi)有一點
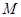
,請用尺規(guī)作圖畫出點
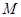
的反演點
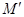
;(保留畫圖痕跡,不必寫畫法).
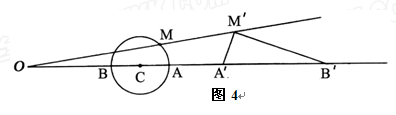
⑶如果一個圖形上各點經(jīng)過反演變換得到的反演點組成另一個圖形,那么這兩個圖形叫做互為反演圖形.已知基圓

的半徑為
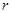
,另一個半徑為

的⊙
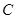
,作射線
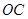
交⊙
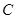
于點
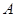
、
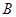
,點
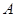
、
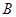
關(guān)于⊙

的反演點分別是
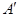
、
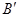
,點
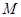
為⊙
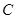
上另一點,關(guān)于⊙

的反演點為
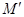
.求證:∠
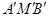
=90°.
查看答案和解析>>
科目:初中數(shù)學(xué)
來源:不詳
題型:單選題
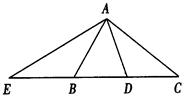
如圖所示,在△
ABC中∠
BAC=90°,
D是
BC中點,
AE⊥
AD交
CB延長線于
E點,則下列結(jié)論正確的是( )
| A.△AED∽△ACB | B.△AEB∽△ACD |
| C.△BAE∽△ACE | D.△AEC∽△DAC |
查看答案和解析>>
科目:初中數(shù)學(xué)
來源:不詳
題型:填空題
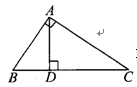
△ABC中,∠BAC=90°AD⊥BC于D,若AB=2,BC=3,則CD的長=
查看答案和解析>>
科目:初中數(shù)學(xué)
來源:不詳
題型:單選題
如圖,
AB∥
CD,
AC、
BD交于
O,
BO=7,
DO=3,
AC=25,則
AO長為( )

查看答案和解析>>
科目:初中數(shù)學(xué)
來源:不詳
題型:解答題
(本小題滿分12分)
如圖,
RtΔ
ABC中,∠
ACB=90°,
AC=4,
BA=5,點
P是
AC上的動點(
P不與
A、C重合)
PQ⊥
AB,垂足為
Q.設(shè)
PC=x,
PQ= y.

小題1:⑴求
y與
x的函數(shù)關(guān)系式;
小題2:⑵試確定此
RtΔ
ABC內(nèi)切圓
I的半徑,并探求
x為何值時,直線
PQ與這個內(nèi)切圓
I相切?
小題3:⑶若0<
x<1,試判斷以
P為圓心,半徑為
y的圓與⊙
I能否相內(nèi)切,若能求出相應(yīng)的
x的值,若不能,請說明理由.
查看答案和解析>>




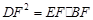 .
.
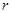 的⊙
的⊙ ,對于任意點
,對于任意點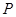 ,在射線
,在射線 上取一點
上取一點 ,使得
,使得 ·
·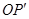 =
=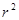 ,這種把點
,這種把點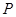 變?yōu)辄c
變?yōu)辄c 的變換叫做反演變換,點
的變換叫做反演變換,點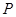 與點
與點 叫做互為反演點,⊙
叫做互為反演點,⊙ 稱為基圓.
稱為基圓.
 內(nèi)有不同的兩點
內(nèi)有不同的兩點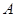 、
、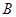 ,它們的反演點分別是
,它們的反演點分別是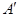 、
、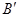 ,則與∠
,則與∠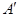 一定相等的角是( ▲ )
一定相等的角是( ▲ )

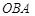
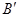
 內(nèi)有一點
內(nèi)有一點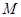 ,請用尺規(guī)作圖畫出點
,請用尺規(guī)作圖畫出點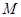 的反演點
的反演點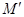 ;(保留畫圖痕跡,不必寫畫法).
;(保留畫圖痕跡,不必寫畫法). 的半徑為
的半徑為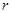 ,另一個半徑為
,另一個半徑為 的⊙
的⊙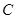 ,作射線
,作射線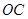 交⊙
交⊙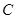 于點
于點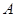 、
、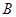 ,點
,點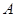 、
、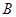 關(guān)于⊙
關(guān)于⊙ 的反演點分別是
的反演點分別是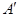 、
、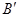 ,點
,點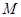 為⊙
為⊙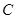 上另一點,關(guān)于⊙
上另一點,關(guān)于⊙ 的反演點為
的反演點為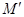 .求證:∠
.求證:∠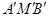 =90°.
=90°.


