
【題目】如圖,已知等邊![]() ,以邊
,以邊![]() 為直徑的半圓與邊
為直徑的半圓與邊![]() ,
,![]() 分別交于點
分別交于點![]() 、
、![]() ,過點
,過點![]() 作
作![]() 于點
于點![]() ,
,
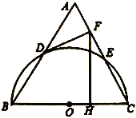
(1)判斷![]() 與
與![]() 的位置關系,并證明你的結論;
的位置關系,并證明你的結論;
(2)過點![]() 作
作![]() 于點
于點![]() ,若等邊
,若等邊![]() 的邊長為8,求
的邊長為8,求![]() ,
,![]() 的長.
的長.
【答案】(1)DF與⊙O相切.理由見解析;(2)![]() ,
,![]() .
.
【解析】
(1)連接OD,如圖,易證△ODB是等邊三角形,則∠DOB=60°,進而可得∠DOB=∠ACB=60°,于是可得OD∥AC,由![]() 可得DO⊥DF,從而可得結論;
可得DO⊥DF,從而可得結論;
(2)連接CD,由CB是⊙O直徑可得DC⊥AB,進而可根據等邊三角形的性質求得AD的長,然后在Rt△ADF中根據30°角的直角三角形的性質即可求出AF的長,進一步即可求出FC的長,然后在Rt△CFH中根據30°角的性質可得CH的長,最后根據勾股定理即可求出結果.
(1)DF與⊙O相切.
證明:連接OD,如圖.
∵△ABC是等邊三角形,
∴∠A=∠B=∠ACB=60°,
∵OD=OB,
∴△ODB是等邊三角形,
∴∠DOB=60°,
∴∠DOB=∠ACB=60°,
∴OD∥AC.
∵DF⊥AC,
∴DO⊥DF,
∴DF與⊙O相切;
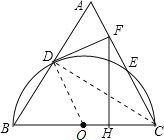
(2)解:連接CD,
∵CB是⊙O直徑,∴DC⊥AB.
又∵AC=CB=AB,
∴D是AB中點,
∴![]() .
.
在直角△ADF中,∠A=60°,∠AFD=90°,則∠ADF=30°,
∴![]() ,
,
∴FC=AC﹣AF=8﹣2=6.
∵FH⊥BC,∠C=60°,
∴∠HFC=30°,
∴![]() ,
,
∴![]() .
.


科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,函數y=![]() (x>0)的圖象G經過點A(4,1),直線l:y=
(x>0)的圖象G經過點A(4,1),直線l:y=![]() +b與圖象G交于點B,與y軸交于點C.
+b與圖象G交于點B,與y軸交于點C.
(1)求k的值;
(2)橫、縱坐標都是整數的點叫做整點.記圖象G在點A,B之間的部分與線段OA,OC,BC圍成的區域(不含邊界)為W.
①當b=﹣1時,直接寫出區域W內的整點個數;
②若區域W內恰有4個整點,結合函數圖象,求b的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD是邊長為2,一個銳角等于60°的菱形紙片,小芳同學將一個三角形紙片的一個頂點與該菱形頂點D重合,按順時針方向旋轉三角形紙片,使它的兩邊分別交CB、BA(或它們的延長線)于點E、F,∠EDF=60°,當CE=AF時,如圖1小芳同學得出的結論是DE=DF.
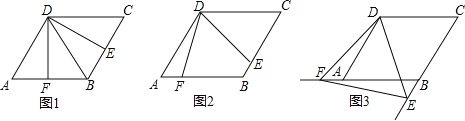
(1)繼續旋轉三角形紙片,當CE≠AF時,如圖2小芳的結論是否成立?若成立,加以證明;若不成立,請說明理由;
(2)再次旋轉三角形紙片,當點E、F分別在CB、BA的延長線上時,如圖3請直接寫出DE與DF的數量關系;
(3)連EF,若△DEF的面積為y,CE=x,求y與x的關系式,并指出當x為何值時,y有最小值,最小值是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖,拋物線![]() 的頂點為
的頂點為![]() ,經過拋物線上的兩點
,經過拋物線上的兩點![]() 和
和![]() 的直線交拋物線的對稱軸于點
的直線交拋物線的對稱軸于點![]() .
.
(1)求拋物線的解析式和直線![]() 的解析式.
的解析式.
(2)在拋物線上![]() 兩點之間的部分(不包含
兩點之間的部分(不包含![]() 兩點),是否存在點
兩點),是否存在點![]() ,使得
,使得![]() ?若存在,求出點
?若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
(3)若點![]() 在拋物線上,點
在拋物線上,點![]() 在
在![]() 軸上,當以點
軸上,當以點![]() 為頂點的四邊形是平行四邊形時,直接寫出滿足條件的點
為頂點的四邊形是平行四邊形時,直接寫出滿足條件的點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
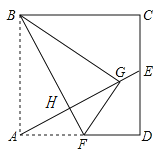
【題目】如圖,點F在正方形ABCD的AD邊上,連接BF.把△ABF沿BF折疊,與△GBF重合.連接AG并延長交CD于點E,交BF于點H.
(1)證明:BF=AE;
(2)若AB=15,EC=7,求GE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
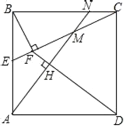
【題目】已知如圖,正方形ABCD的邊長為4,取AB邊上的中點E,連接CE,過點B作BF⊥CE于點F,連接DF.過點A作AH⊥DF于點H,交CE于點M,交BC于點N,則MN=_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
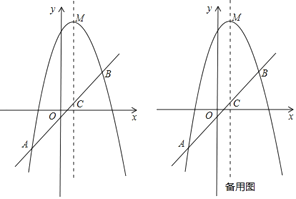
【題目】在平面直角坐標系中,拋物線y=x2+(k﹣1)x﹣k與直線y=kx+1交于A,B兩點,點A在點B的左側.
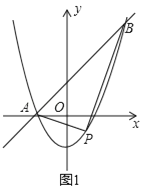

(1)如圖1,當k=1時,直接寫出A,B兩點的坐標;
(2)在(1)的條件下,點P為拋物線上的一個動點,且在直線AB下方,試求出△ABP面積的最大值及此時點P的坐標;
(3)如圖2,拋物線y=x2+(k﹣1)x﹣k(k>0)與x軸交于點C、D兩點(點C在點D的左側),在直線y=kx+1上是否存在唯一一點Q,使得∠OQC=90°?若存在,請求出此時k的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=﹣x2+mx的圖象如圖,對稱軸為直線x=2,若關于x的一元二次方程﹣x2+mx﹣t=0(t為實數)在1<x<5的范圍內有解,則t的取值范圍是( )
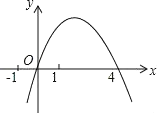
A.t>﹣5B.﹣5<t<3C.3<t≤4D.﹣5<t≤4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com