Question

如圖，在等邊三角形ABC中，BC=6,射線AG∥BC，點E從點A出發沿射線AG以的速度運動，同時點F從點B出發沿射線BC以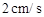的速度運動，設運動時間為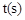

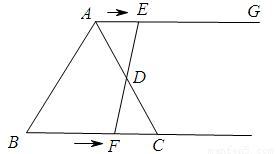
（1）連接EF，當EF經過AC邊的中點D時，求證：△ADE≌△CDF

（2）填空：

①當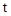為     s時，四邊形ACFE是菱形；

②當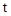為     s時，以A，F，C，E為頂點的四邊形是直角梯形。

 

Answer 1

【答案】

（1）見解析（2）①6 ②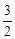

【解析】解：（1）證明：∵AG∥BC，∴∠EAD=∠ACB。

∵D是AC邊的中點，∴AD=CD。

又∵∠ADE=∠CDF ，∴△ADE≌△CDF（ASA）。

（2）①6。

②。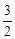

（1）由ASA證明△ADE≌△CDF。

（2）①∵當四邊形ACFE是菱形時，∴AE=AC=CF=EF。

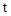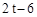由題意可知：AE=，CF=，∴,即。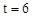

②若EF⊥AG，四邊形ACFE是直角梯形，

過C作CM⊥AG于點M，

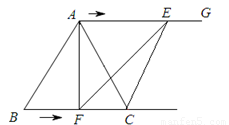
∵AM=3，AE=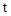，ME=CF=，

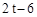∴AE－ME=AM，，即，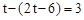

此時，G與F重合，不符合題意，舍去。

若AF⊥BV，四邊形若四邊形AFCE是直角梯形，

∵△ABC是等邊三角形，F是BC中點，

∴，解得。

經檢驗，符合題意。