
如圖,在⊙O中,∠ACB=∠BDC=60°,AC=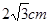 ,
,
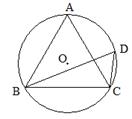
(1)判斷△ABC的形狀并證明你的結論;
(2)求⊙O的周長
(1)見解析(1)4π
【解析】
試題分析:利用圓周角定理可得∠BAC=∠CPB,∠ABC=∠APC,而∠APC=∠CPB=60°,所以∠BAC=∠ABC=60°,從而可判斷△ABC的形狀(2)由三角形內角和得∠ABC=60°,所以△ABC是等邊三角形,作OE⊥AC,連接OA,由垂徑定理得,AE=CE=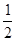 AC=
AC=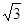 cm,再由余弦的概念求得半徑OA的長,由圓的周長公式求得周長.
cm,再由余弦的概念求得半徑OA的長,由圓的周長公式求得周長.
解:(1)△ABC為等邊三角形證明如下:
∵∠BAC和∠BDC都是弧BC所對的圓周角
∴∠BAC=∠BDC
∵∠ACB=∠BDC=60° ∴∠BAC =∠ACB =60°
∴△ABC為等邊三角形……………………3分
(2)過O點作OE⊥AC于E點,連接OA
∵AC=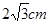 ∴AE=CE=
∴AE=CE=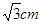
∵△ABC為等邊三角形
∴∠OAE=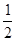 ∠BAC=30° 設OE=x,則OA=2x,
∠BAC=30° 設OE=x,則OA=2x,
在Rt△OAE中,有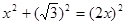 ,解之得x=1
,解之得x=1
∴OA=2 即⊙O的周長=2×2×π=4πcm
考點:圓周角定理;圓心角、弧、弦的關系;等邊三角形的性質;圓的認識;解直角三角形.
點評:本題考查了圓周角定理.同弧所對的圓周角相等,并且等于它所對的圓心角的一半.也考查了等邊三角形的判定方法.本題利用了圓周角定理,等邊三角形的判定和性質,垂徑定理,余弦的概念,圓周長公式求解.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
 19、如圖,在△ABC中,CD⊥AB于D,FG⊥AB于G,ED∥BC,試說明∠1=∠2,以下是證明過程,請填空:
19、如圖,在△ABC中,CD⊥AB于D,FG⊥AB于G,ED∥BC,試說明∠1=∠2,以下是證明過程,請填空:查看答案和解析>>
科目:初中數學 來源: 題型:
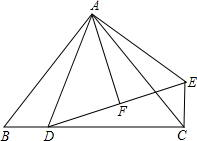 如圖,在△ABC中,已知AB=AC,∠BAC=90°,D是BC上一點,EC⊥BC,EC=BD,DF=FE.求證:
如圖,在△ABC中,已知AB=AC,∠BAC=90°,D是BC上一點,EC⊥BC,EC=BD,DF=FE.求證:查看答案和解析>>
科目:初中數學 來源: 題型:
 15、如圖,在△ABC中,AQ=PQ,PR=PS,PS⊥AC于S,PR⊥AB于R,則以下結論中:(1)AS=AR;(2)△BRP∽△QSP;(3)PQ∥AB中,正確的有
15、如圖,在△ABC中,AQ=PQ,PR=PS,PS⊥AC于S,PR⊥AB于R,則以下結論中:(1)AS=AR;(2)△BRP∽△QSP;(3)PQ∥AB中,正確的有查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com