
【題目】如圖,點A(m,6),B(n,1)在反比例函數圖象上,AD⊥x軸于點D,BC⊥x軸于點C,DC=5.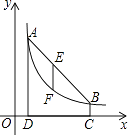
(1)求m,n的值并寫出反比例函數的表達式;
(2)連接AB,E是線段AB上一點,過點E作x軸的垂線,交反比例函數圖象于點F,若EF= ![]() AD,求出點E的坐標.
AD,求出點E的坐標.
【答案】
(1)解:設反比例函數的解析式為y= ![]() ,
,
把(n,1)代入得:k=n,
即y= ![]() ,
,
∵點A(m,6),B(n,1)在反比例函數圖象上,AD⊥x軸于點D,BC⊥x軸于點C,DC=5,
∴ ![]() ,
,
解得:m=1,n=6,
即A(1,6),B(6,1);
反比例函數的解析式為:y= ![]()
(2)解:設直線AB的解析式為y=ax+b,
把A(1,6)和B(6,1)代入得: ![]() ,
,
解得:a=﹣1,b=7,
即直線AB的解析式為:y=﹣x+7,
設E點的橫坐標為m,則E(m,﹣m+7),F(m, ![]() ),
),
∴EF=﹣m+7﹣ ![]() ,
,
∵EF= ![]() AD,
AD,
∴﹣m+7﹣ ![]() =
= ![]() ,
,
解得:m=2,m2=3,
經檢驗都是原方程的解,
即E的坐標為(2,5)或(3,4)
【解析】(1) 首先把B點的坐標代入得出K=n, 用待定系數法得出關于M,N的方程組,求解即得出m,n的值及A、B兩點的坐標;(2)設直線AB的解析式為y=ax+b,把A(1,6)和B(6,1)代入得關于a,b的方程組,求出a=﹣1,b=7,從而得出直線AB的解析式為:y=﹣x+7,設E點的橫坐標為m,從而表示出E、F點的坐標,根據EF的長度得出關于m的方程求解即得出E點的坐標。
【考點精析】解答此題的關鍵在于理解確定一次函數的表達式的相關知識,掌握確定一個一次函數,需要確定一次函數定義式y=kx+b(k不等于0)中的常數k和b.解這類問題的一般方法是待定系數法.


 品學雙優卷系列答案
品學雙優卷系列答案 小學期末沖刺100分系列答案
小學期末沖刺100分系列答案 期末復習檢測系列答案
期末復習檢測系列答案 超能學典單元期中期末專題沖刺100分系列答案
超能學典單元期中期末專題沖刺100分系列答案 黃岡360度定制密卷系列答案
黃岡360度定制密卷系列答案科目:初中數學 來源: 題型:
【題目】(本題滿分8分)
如圖,點E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF與DE交于點O.

(1)求證:AB=DC;
(2)試判斷△OEF的形狀,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為表彰在美術展覽活動中獲獎的同學,老師決定購買一些水筆和顏料盒作為獎品,請你根據圖中所給的信息,解答下列問題; 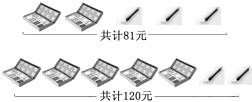
(1)求出每個顏料盒,每支水筆各多少元?
(2)若學校計劃購買顏料盒和水筆共20個,所用費用不超過340元,則顏料盒至多購買多少個?
(3)恰逢商店舉行優惠促銷活動,具體辦法如下:顏料盒按七折優惠,水筆10支以上超出部分按八折優惠,若學校決定購買同種數量的同一獎品,并且該獎品的數量超過10件,請你幫助分析,購買顏料盒合算還是購買水筆合算.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,△![]() 為等邊三角形,O為坐標原點,點A關于y軸的對稱點為D,連接AD,BD,OD,其中AD,BD分別交y軸于點E,P.
為等邊三角形,O為坐標原點,點A關于y軸的對稱點為D,連接AD,BD,OD,其中AD,BD分別交y軸于點E,P.
(1)如圖1,若點B在x軸的負半軸上時,直接寫出![]() 的度數;
的度數;
(2)如圖2,將△![]() 繞點O旋轉,且點A始終在第二象限,此時AO與y軸正半軸夾角為
繞點O旋轉,且點A始終在第二象限,此時AO與y軸正半軸夾角為![]() ,60<
,60<![]() <90,依題意補全圖形,并求出
<90,依題意補全圖形,并求出![]() 的度數;(用含
的度數;(用含![]() 的式子表示)
的式子表示)
(3)在第(2)問的條件下,用等式表示線段BP,PE,PO之間的數量關系.(直接寫出結果)
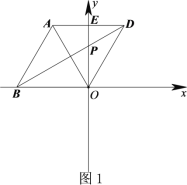
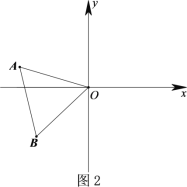
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,D為⊙O上一點,點C在直徑BA的延長線上,且∠CDA=∠CBD.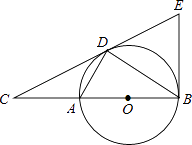
(1)求證:CD是⊙O的切線;
(2)過點B作⊙O的切線交CD的延長線于點E,BC=6, ![]() .求BE的長.
.求BE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】你會求(a﹣1)(a2012+a2011+a2010+…+a2+a+1)的值嗎?這個問題看上去很復雜,我們可以先考慮簡單的情況,通過計算,探索規律:
![]() ,
,
![]() ,
,
![]() ,
,
(1)由上面的規律我們可以大膽猜想,得到(a﹣1)(a2014+a2013+a2012+…+a2+a+1)=
利用上面的結論,求:
(2)22014+22013+22012+…+22+2+1的值是 .
(3)求52014+52013+52012+…+52+5+1的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90![]() ,∠BAC的平分線交BC于D,過點C作CG⊥AB于G,交AD于E,過點D作DF⊥AB于F.下列結論①∠CED=
,∠BAC的平分線交BC于D,過點C作CG⊥AB于G,交AD于E,過點D作DF⊥AB于F.下列結論①∠CED= ![]() ;②
;②![]() ;③∠ADF=
;③∠ADF= ![]() ;④CE=DF.正確的是( )
;④CE=DF.正確的是( )
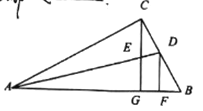
A. ①②④ B. ②③④ C. ①③ D. ①②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖1是一個長為![]() ,寬為
,寬為![]() 的長方形,沿圖中虛線用剪刀均勻分成四塊小長方形,然后按圖2形狀拼成一個正方形.
的長方形,沿圖中虛線用剪刀均勻分成四塊小長方形,然后按圖2形狀拼成一個正方形.
(1)請用兩種不同方法,求圖2中陰影部分的面積(不用化簡)
方法1:____________________
方法2:____________________
(2)觀察圖2,寫出![]() ,
,![]() ,
,![]() 之間的等量關系,并驗證;
之間的等量關系,并驗證;

(3)根據(2)題中的等量關系,解決如下問題:
①若![]() ,
,![]() ,求
,求![]() 的值;
的值;
②若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com