
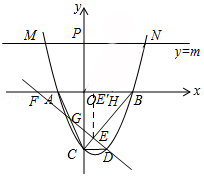
【題目】如圖,在平面直角坐標系中,已知拋物線y= ![]() x2+bx+c與x軸交于A(﹣1,0),B(2,0)兩點,與y軸交于點C.
x2+bx+c與x軸交于A(﹣1,0),B(2,0)兩點,與y軸交于點C.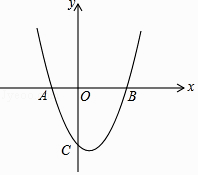
(1)求該拋物線的解析式;
(2)直線y=﹣x+n與該拋物線在第四象限內交于點D,與線段BC交于點E,與x軸交于點F,且BE=4EC.
①求n的值;
②連接AC,CD,線段AC與線段DF交于點G,△AGF與△CGD是否全等?請說明理由;
(3)直線y=m(m>0)與該拋物線的交點為M,N(點M在點N的左側),點 M關于y軸的對稱點為點M',點H的坐標為(1,0).若四邊形OM'NH的面積為 ![]() .求點H到OM'的距離d的值.
.求點H到OM'的距離d的值.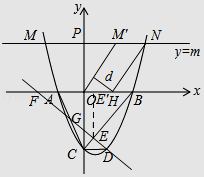
【答案】
(1)
解:∵拋物線y= ![]() x2+bx+c與x軸交于A(﹣1,0),B(2,0)兩點,
x2+bx+c與x軸交于A(﹣1,0),B(2,0)兩點,
∴ 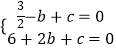 ,解得
,解得 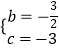 ,
,
∴該拋物線的解析式y= ![]() x2﹣
x2﹣ ![]() x﹣3;
x﹣3;
(2)
解:①如圖,過點E作EE'⊥x軸于E',則EE'∥OC,
∴ ![]() =
= ![]() ,
,
∵BE=4EC,
∴BE'=4OE',
設點E的坐標為(x,y),則OE'=x,BE'=4x,
∵B(2,0),
∴OB=2,即x+4x=2,
∴x= ![]() ,
,
∵拋物線y= ![]() x2﹣
x2﹣ ![]() x﹣3與y軸交于點C,
x﹣3與y軸交于點C,
∴C(0,﹣3),
設直線BC的解析式為y=kx+b',
∵B(2,0),C(0,﹣3),
∴ ![]() ,解得
,解得 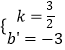 ,
,
∴直線BC的解析式為y= ![]() x﹣3,
x﹣3,
當x= ![]() 時,y=﹣
時,y=﹣ ![]() ,
,
∴E( ![]() ,﹣
,﹣ ![]() ),
),
把E的坐標代入直線y=﹣x+n,可得﹣ ![]() +n=﹣
+n=﹣ ![]() ,
,
解得n=﹣2;
②△AGF與△CGD全等.理由如下:
∵直線EF的解析式為y=﹣x﹣2,
∴當y=0時,x=﹣2,
∴F(﹣2,0),OF=2,
∵A(﹣1,0),
∴OA=1,
∴AF=2﹣1=1,
由 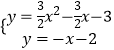 解得
解得 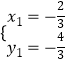 ,
, ![]() ,
,
∵點D在第四象限,
∴點D的坐標為(1,﹣3),
∵點C的坐標為(0,﹣3),
∴CD∥x軸,CD=1,
∴∠AFG=∠CDG,∠FAG=∠DCG,
∴△AGF≌△CGD;
(3)
解:∵拋物線的對稱軸為x=﹣ ![]() =
= ![]() ,直線y=m(m>0)與該拋物線的交點為M,N,
,直線y=m(m>0)與該拋物線的交點為M,N,
∴點M、N關于直線x= ![]() 對稱,
對稱,
設N(t,m),則M(1﹣t,m),
∵點 M關于y軸的對稱點為點M',
∴M'(t﹣1,m),
∴點M'在直線y=m上,
∴M'N∥x軸,
∴M'N=t﹣(t﹣1)=1,
∵H(1,0),
∴OH=1=M'N,
∴四邊形OM'NH是平行四邊形,
設直線y=m與y軸交于點P,
∵四邊形OM'NH的面積為 ![]() ,
,
∴OH×OP=1×m= ![]() ,即m=
,即m= ![]() ,
,
∴OP= ![]() ,
,
當 ![]() x2﹣
x2﹣ ![]() x﹣3=
x﹣3= ![]() 時,解得x1=﹣
時,解得x1=﹣ ![]() ,x2=
,x2= ![]() ,
,
∴點M的坐標為(﹣ ![]() ,
, ![]() ),
),
∴M'( ![]() ,
, ![]() ),即PM'=
),即PM'= ![]() ,
,
∴Rt△OPM'中,OM'= ![]() =
= ![]() ,
,
∵四邊形OM'NH的面積為 ![]() ,
,
∴OM'×d= ![]() ,
,
∴d= ![]() .
.
【解析】(1)根據拋物線y= ![]() x2+bx+c與x軸交于A(﹣1,0),B(2,0)兩點,可得拋物線的解析式;(2)①過點E作EE'⊥x軸于E',則EE'∥OC,根據平行線分線段成比例定理,可得BE'=4OE',設點E的坐標為(x,y),則OE'=x,BE'=4x,根據OB=2,可得x=
x2+bx+c與x軸交于A(﹣1,0),B(2,0)兩點,可得拋物線的解析式;(2)①過點E作EE'⊥x軸于E',則EE'∥OC,根據平行線分線段成比例定理,可得BE'=4OE',設點E的坐標為(x,y),則OE'=x,BE'=4x,根據OB=2,可得x= ![]() ,再根據直線BC的解析式為y=
,再根據直線BC的解析式為y= ![]() x﹣3,即可得到E(
x﹣3,即可得到E( ![]() ,﹣
,﹣ ![]() ),把E的坐標代入直線y=﹣x+n,可得n的值;②根據F(﹣2,0),A(﹣1,0),可得AF=1,再根據點D的坐標為(1,﹣3),點C的坐標為(0,﹣3),可得CD∥x軸,CD=1,再根據∠AFG=∠CDG,∠FAG=∠DCG,即可判定△AGF≌△CGD;(3)根據軸對稱的性質得出OH=1=M'N,進而判定四邊形OM'NH是平行四邊形,再根據四邊形OM'NH的面積為
),把E的坐標代入直線y=﹣x+n,可得n的值;②根據F(﹣2,0),A(﹣1,0),可得AF=1,再根據點D的坐標為(1,﹣3),點C的坐標為(0,﹣3),可得CD∥x軸,CD=1,再根據∠AFG=∠CDG,∠FAG=∠DCG,即可判定△AGF≌△CGD;(3)根據軸對稱的性質得出OH=1=M'N,進而判定四邊形OM'NH是平行四邊形,再根據四邊形OM'NH的面積為 ![]() ,求得OP=
,求得OP= ![]() ,再根據點M的坐標為(﹣
,再根據點M的坐標為(﹣ ![]() ,
, ![]() ),得到PM'=
),得到PM'= ![]() ,Rt△OPM'中,運用勾股定理可得OM'=
,Rt△OPM'中,運用勾股定理可得OM'= ![]() ,最后根據OM'×d=
,最后根據OM'×d= ![]() ,即可得到d=
,即可得到d= ![]() .
.
【考點精析】根據題目的已知條件,利用二次函數的性質的相關知識可以得到問題的答案,需要掌握增減性:當a>0時,對稱軸左邊,y隨x增大而減小;對稱軸右邊,y隨x增大而增大;當a<0時,對稱軸左邊,y隨x增大而增大;對稱軸右邊,y隨x增大而減小.


科目:初中數學 來源: 題型:
【題目】如圖(1),Rt△AOB中,∠A=90°,∠AOB=60°,OB=![]() ,∠AOB的平分線OC交AB于C,過O點做與OB垂直的直線ON.動點P從點B出發沿折線BC﹣CO以每秒1個單位長度的速度向終點O運動,運動時間為t秒,同時動點Q從點C出發沿折線CO﹣ON以相同的速度運動,當點P到達點O時P、Q同時停止運動.
,∠AOB的平分線OC交AB于C,過O點做與OB垂直的直線ON.動點P從點B出發沿折線BC﹣CO以每秒1個單位長度的速度向終點O運動,運動時間為t秒,同時動點Q從點C出發沿折線CO﹣ON以相同的速度運動,當點P到達點O時P、Q同時停止運動.
(1)求OC、BC的長;
(2)設△CPQ的面積為S,求S與t的函數關系式;
(3)當P在OC上Q在ON上運動時,如圖(2),設PQ與OA交于點M,當t為何值時,△OPM為等腰三角形?求出所有滿足條件的t值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小剛在課外書中看到這樣一道有理數的混合運算題:
計算:![]()
她發現,這個算式反映的是前后兩部分的和,而這兩部分之間存在著某種關系,利用這種關系,他順利地解答了這道題。
(1)前后兩部分之間存在著什么關系?
(2)先計算哪步分比較簡便?并請計算比較簡便的那部分。
(3)利用(1)中的關系,直接寫出另一部分的結果。
(4)根據以上分析,求出原式的結果。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)探究證明:
在△ABC中,∠ACB=90°,AC=BC,直線MN經過點C,且AD⊥MN于點D,BE⊥MN于點E,當直線MN繞點C旋轉到圖1的位置時,求證:DE=AD+BE;
(2)發現探究:
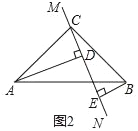
當直線MN繞點C旋轉到圖2的位置時,(1)中的結論是否成立,如果不成立,DE、AD、BE應滿足的關系是_____.
(3)解決問題:
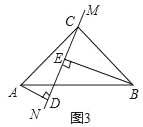
當直線MN繞點C旋轉到圖3的位置時,若BE=8,AD=2,請直接寫出DE的長為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
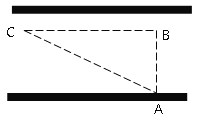
【題目】“道路交通管理條例”規定:小汽車在城街上行駛速度不得超過70千米/小時,如圖,一輛小汽車在一條城市街路上直道行駛,某一時刻剛好行駛到路面對車速檢測儀A正前方30米B處,過了2秒后,測得小汽車C與車速檢測儀A間距離為50米,這輛小汽車超速了嗎?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了更好改善河流的水質,治污公司決定購買10臺污水處理設備![]() 現有A,B兩種型號的設備,其中每臺的價格,月處理污水量如下表:經調查:購買一臺A型設備比購買一臺B型設備多2萬元,購買2臺A型設備比購買3臺B型設備少6萬元.
現有A,B兩種型號的設備,其中每臺的價格,月處理污水量如下表:經調查:購買一臺A型設備比購買一臺B型設備多2萬元,購買2臺A型設備比購買3臺B型設備少6萬元.
A型 | B型 | |
價格 | a | b |
處理污水量 | 240 | 200 |
![]() 求a,b的值;
求a,b的值;
![]() 治污公司經預算購買污水處理設備的資金不超過105萬元,你認為該公司有哪幾種購買方案;
治污公司經預算購買污水處理設備的資金不超過105萬元,你認為該公司有哪幾種購買方案;
![]() 在
在![]() 的條件下,若每月要求處理污水量不低于2040噸,為了節約資金,請你為治污公司設計一種最省錢的購買方案.
的條件下,若每月要求處理污水量不低于2040噸,為了節約資金,請你為治污公司設計一種最省錢的購買方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線AB與CD相交于點O,OE平分∠AOD,OF平分∠BOD.
(1)若∠AOC=70°,求∠DOE和∠EOF的度數;
(2)請寫出圖中∠AOD的補角和∠AOE的余角.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】梅嶺中學為了解“課程選修”的情況,對報名參加“藝術欣賞”,“科技制作”,“數學思維”,“閱讀寫作”這四個選修項目的學生(每人限報一課)進行抽樣調查,下面是根據收集的數據繪制的不完整的統計圖,請根據圖中提供的信息,解答下面的問題:
(1)此次共調查了______名學生,扇形統計圖中“藝術欣賞”部分的圓心角是______度;
(2)請把這個條形統計圖補充完整;
(3)現該校共有800名學生報名參加這四個選修項目,請你估計其中有多少名學生選修 “科技制作”項目.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com