
【題目】如圖所示,線段![]() cm,點C從點P出發以1cm/s的速度沿AB向左運動,點D從點B出發以2cm/s的速度沿AB向左運動(點C在線段AP上,D在線段BP上)
cm,點C從點P出發以1cm/s的速度沿AB向左運動,點D從點B出發以2cm/s的速度沿AB向左運動(點C在線段AP上,D在線段BP上)
(1)若C,D 運動到任意時刻都有PD=2AC,試說明PB=2AP;
(2)在(1)的條件下,Q是直線AB上一點,若AQ-BQ=PQ,求PQ的值;
(3)在(1)的條件下,若C,D運動了一段時間后恰有AB=2CD,這時點C停止運動,點D繼續在線段PB上運動,M,N 分別是CD,PD的中點,求MN的值.
![]()
【答案】(1)見解析;(2)PQ=2m或6cm;(3)MN=![]() 。
。
【解析】
(1)根據C、D的運動速度知BD=2PC,再由已知條件PD=2AC求得PB=2AP,所以點P在線段AB上的![]() 處;
處;
(2)由題設畫出圖示,根據AQ-BQ=PQ求得AQ=PQ+BQ;然后求得AP=BQ,從而求得PQ與AB的關系;
(3)當C點停止運動時,有CD=![]() AB,故AC+BD=
AB,故AC+BD=![]() AB,再設BD=a,PD=4-a,CD=5-a即可列式得出答案.
AB,再設BD=a,PD=4-a,CD=5-a即可列式得出答案.
(1) 根據 C,D 的運動速度知:BD=2PC
又∵PD=2AC,
![]() BD+PD=2(PC+AC) ,即 PB=2AP.
BD+PD=2(PC+AC) ,即 PB=2AP.
(2) 如圖:
![]()
![]() AQ-BQ=PQ,
AQ-BQ=PQ,
![]() AQ=PQ+BQ ;
AQ=PQ+BQ ;
![]() AQ=AP+PQ ,
AQ=AP+PQ ,
![]() AP=BQ,
AP=BQ,
![]() PQ=
PQ=![]() AB=2cm ;
AB=2cm ;
當點 Q 在 AB 的延長線上時,如圖,
![]()
![]() AQ-AB=PQ ,且AQ-BQ=PQ ,AP=BQ,
AQ-AB=PQ ,且AQ-BQ=PQ ,AP=BQ,
![]() AQ-BQ=PQ=AB=6cm .
AQ-BQ=PQ=AB=6cm .
綜上所述,PQ=2cm或PQ=6cm .
(3)
![]()
當 C 點停止運動時,有 CD=![]() AB=3cm,
AB=3cm,
![]() AC+BD=
AC+BD=![]() AB=3cm ,
AB=3cm ,
D點繼續運動,
設BD=a,PD=4-a,CD=5-a
![]()
![]()


 心算口算巧算一課一練系列答案
心算口算巧算一課一練系列答案科目:初中數學 來源: 題型:
【題目】甲乙兩地相距200km,快車速度為120![]() ,慢車速度為80
,慢車速度為80![]() ,慢車從甲地出發,快車從乙地出發,
,慢車從甲地出發,快車從乙地出發,
(1)如果兩車同時出發,相向而行,出發后幾時兩車相遇?相遇時離甲地多遠?
(2)如果兩車同時出發,同向(從乙開始向甲方向)而行,出發后幾時兩車相遇?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在數軸上點A表示的有理數為﹣6,點B表示的有理數為6,點P從點A出發以每秒4個單位長度的速度在數軸上由A向B運動,當點P到達點B后立即返回,仍然以每秒4個單位長度的速度運動至點A停止運動,設運動時間為t(單位:秒).
(1)求t=1時點P表示的有理數;
(2)求點P與點B重合時的t值;
(3)在點P沿數軸由點A到點B再回到點A的運動過程中,求點P與點A的距離(用含t的代數式表示);
(4)當點P表示的有理數與原點的距離是2個單位長度時,請求出所有滿足條件的t值.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料:
點A、B在數軸上分別表示兩個數a、b,A、B兩點間的距離記為|AB|,O表示原點.當A、B兩點中有一點在原點時,不妨設點A為原點,如圖1,則|AB|=|OB|=|b|=|a-b|;當A、B兩點都不在原點時,

①如圖2,若點A、B都在原點的右邊時,|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|;
②如圖3,若點A、B都在原點的左邊時,|AB|=|OB|-|OA|=|b|-|a|=-b-(-a)=|a-b|;
③如圖4,若點A、B在原點的兩邊時,|AB|=|OB|+|OA|=|b|+|a|=-b+a=|a-b|.
回答下列問題:
(1)綜上所述,數軸上A、B兩點間的距離為|AB|=______.
(2)若數軸上的點A表示的數為3,點B表示的數為-4,則A、B兩點間的距離為______;
(3)若數軸上的點A表示的數為x,點B表示的數為-2,則|AB|=______,若|AB|=3,則x的值為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
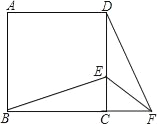
【題目】如圖,正方形ABCD中,E為CD邊上一點,F為BC延長線上一點,CE=CF.
(1)求證:△BCE≌△DCF;
(2)若∠BEC=60°,求∠EFD的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的頂點P是BC中點,PE,PF分別交AB,AC于點E,F,給出下列四個結論:①△APE≌△CPF;②AE=CF;③△EAF是等腰直角三角形;④S△ABC=2S四邊形AEPF,上述結論正確的有( )

A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在△ABC中,AB=AC,點D是BC的中點,點E在AD上.

(1)求證:BE=CE;
(2)如圖2,若BE的延長線交AC于點F,且BF⊥AC,垂足為F,∠BAC=45°,原題設其它條件不變.求證:△AEF≌△BCF.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,OM是∠AOC的平分線,ON是∠BOC的平分線.
(1)如圖1,當∠AOB是直角,∠BOC=60°時,∠MON的度數是多少?
(2)如圖2,當∠AOB=α,∠BOC=60°時,猜想∠MON與α的數量關系;
(3)如圖3,當∠AOB=α,∠BOC=β時,猜想∠MON與α、β有數量關系嗎?如果有,指出結論并說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com