
 請把以下證明過程補充完整,并在下面的括號內填上推理理由:
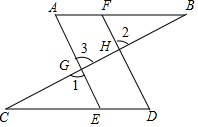
請把以下證明過程補充完整,并在下面的括號內填上推理理由:分析 先根據題意得出∠2=∠3,故可得出AE∥FD,故∠A=∠BFD,再由∠A=∠D可得出∠D=∠BFD,
故可得出AB∥CD,進而可得出結論.
解答 證明:∵∠1=∠2(已知),
又∵∠1=∠3對頂角相等,
∴∠2=∠3(等量代換),
∴AE∥FD (同位角相等,兩直線平行),
∴∠A=∠BFD (兩直線平行,同位角相等).
∵∠A=∠D(已知),
∴∠D=∠BFD(等量代換),
∴AB∥CD (內錯角相等,兩直線平行).
∴∠B=∠C (兩直線平行,內錯角相).
故答案為:對頂角相等;∠3;同位角相等,兩直線平行;兩直線平行,同位角相等;∠BFD;AB,內錯角相等,兩直線平行;兩直線平行,內錯角相等.
點評 本題考查的是平行線的判定與性質,熟知平行線的判定定理是解答此題的關鍵.


 課程達標測試卷闖關100分系列答案
課程達標測試卷闖關100分系列答案 新卷王期末沖刺100分系列答案
新卷王期末沖刺100分系列答案 全能闖關100分系列答案
全能闖關100分系列答案科目:初中數學 來源: 題型:選擇題
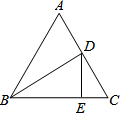 如圖,在等邊△ABC中,BD平分∠ABC交AC于點D,過點D作DE⊥BC于點E,且CE=1.5,則AB的長為( )
如圖,在等邊△ABC中,BD平分∠ABC交AC于點D,過點D作DE⊥BC于點E,且CE=1.5,則AB的長為( )| A. | 3 | B. | 4.5 | C. | 6 | D. | 7.5 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,飛機飛行高度BC為1500m,飛行員看地平面指揮塔A的俯角為α,則飛機與指揮塔A的距離為( ) m.
如圖,飛機飛行高度BC為1500m,飛行員看地平面指揮塔A的俯角為α,則飛機與指揮塔A的距離為( ) m.| A. | $\frac{1500}{sinα}$ | B. | 1500sinα | C. | 1500cosα | D. | $\frac{1500}{tanα}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
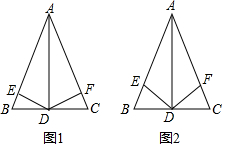 (1)如圖1:在△ABC中,AB=AC,AD⊥BC,DE⊥AB于點E,DF⊥AC于點F.證明:DE=DF.
(1)如圖1:在△ABC中,AB=AC,AD⊥BC,DE⊥AB于點E,DF⊥AC于點F.證明:DE=DF.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
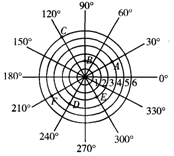 如圖,雷達探測器測得六個目標A,B,C,D,E,F出現按照規定的目標表示方法,目標E,F的位置表示為E(3,300°),F(5,210°),按照此方法在表示目標A,B,D,E的位置時,其中表示不正確的是( )
如圖,雷達探測器測得六個目標A,B,C,D,E,F出現按照規定的目標表示方法,目標E,F的位置表示為E(3,300°),F(5,210°),按照此方法在表示目標A,B,D,E的位置時,其中表示不正確的是( )| A. | A(4,30°) | B. | B(2,90°) | C. | C(6,120°) | D. | D(3,240°) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com