
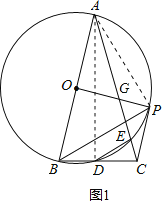
【題目】如圖,在△ABC中,AB=AC,∠A=30°,AB=10,以AB為直徑的⊙O交BC于點D,交AC于點E,連接DE,過點B作BP平行于DE,交⊙O于點P,連接CP、OP.

(1)求證:點D為BC的中點;
(2)求AP的長度;
(3)求證:CP是⊙O的切線.
【答案】(1)BD=DC;(2)5![]() ;(3)詳見解析.
;(3)詳見解析.
【解析】
(1)連接AD,由圓周角定理可知∠ADB=90°,證得結論;
(2)根據等腰三角形的性質得到AD平分∠BAC,即∠BAD=∠CAD,可得![]() ,則BD=DE,所以BD=DE=DC,得到∠DEC=∠DCE,在等腰△ABC中可計算出∠ABC=75°,故∠DEC=75°,再由三角形內角和定理得出∠EDC的度數,再根據BP∥DE可知∠PBC=∠EDC=30°,進而得出∠ABP的度數,然后利用OB=OP,可知∠OBP=∠OPB,由三角形內角和定理即可得出∠BOP=90°,則△AOP是等腰直角三角形,易得AP的長度;
,則BD=DE,所以BD=DE=DC,得到∠DEC=∠DCE,在等腰△ABC中可計算出∠ABC=75°,故∠DEC=75°,再由三角形內角和定理得出∠EDC的度數,再根據BP∥DE可知∠PBC=∠EDC=30°,進而得出∠ABP的度數,然后利用OB=OP,可知∠OBP=∠OPB,由三角形內角和定理即可得出∠BOP=90°,則△AOP是等腰直角三角形,易得AP的長度;
(3)設OP交AC于點G,由∠BOP=90°可知∠AOG=90°,在Rt△AOG中,由∠OAG=30°可得![]() =
=![]() ,由于
,由于![]() =
=![]() =
=![]() ,則
,則![]() =
=![]() ,根據三角形相似的判定可得到△AOG∽△CPG,由相似三角形形的性質可知∠GPC=∠AOG=90°,然后根據切線的判定定理即可得到CP是⊙O的切線.
,根據三角形相似的判定可得到△AOG∽△CPG,由相似三角形形的性質可知∠GPC=∠AOG=90°,然后根據切線的判定定理即可得到CP是⊙O的切線.
(1)BD=DC.理由如下:
如圖1,連接AD,
∵AB是直徑,
∴∠ADB=90°,
∴AD⊥BC.
(2)如圖1,連接AP.
∵AD是等腰△ABC底邊上的中線,
∴∠BAD=∠CAD,
∴![]()
∴BD=DE.
∴BD=DE=DC,
∴∠DEC=∠DCE,
△ABC中,AB=AC,∠A=30°,
∴∠DCE=∠ABC=![]() (180°﹣30°)=75°,
(180°﹣30°)=75°,
∴∠DEC=75°,
∴∠EDC=180°﹣75°﹣75°=30°,
∵BP∥DE,
∴∠PBC=∠EDC=30°,
∴∠ABP=∠ABC﹣∠PBC=75°﹣30°=45°,
∵OB=OP,
∴∠OBP=∠OPB=45°,
∴∠BOP=90°.
∴△AOP是等腰直角三角形.
∵AO=![]() AB=5.
AB=5.
∴AP=![]() AO=5
AO=5![]() ;
;
(3)設OP交AC于點G,如圖1,
則∠AOG=∠BOP=90°,
在Rt△AOG中,∠OAG=30°,
∴![]() =
=![]() ,
,
又∵![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴![]() =
=![]() .
.
又∵∠AGO=∠CGP,
∴△AOG∽△CPG,
∴∠GPC=∠AOG=90°,
∴OP⊥PC,
∴CP是⊙O的切線.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
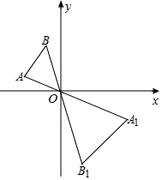
【題目】如圖,已知△AOB和△A1OB1是以點O為位似中心的位似圖形,且△AOB和△A1OB1的周長之比為1:2,點B的坐標為(-1,2),則點B1的坐標為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,點A(3,3),點B(4,0),點C(0,﹣1).

(1)以點C為中心,把△ABC逆時針旋轉90°,請在圖中畫出旋轉后的圖形△A′B′C,點B′的坐標為________;
(2)在(1)的條件下,求出點A經過的路徑![]() 的長(結果保留π).
的長(結果保留π).
查看答案和解析>>
科目:初中數學 來源: 題型:
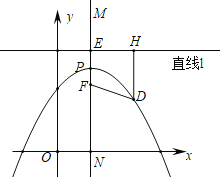
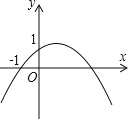
【題目】尋找神奇點!每條拋物線內都有一個神奇的點F(也叫焦點),還有一條與之配套的直線!(也叫準線),使得拋物線上的每個點到F的距離等于到直線l的距離.如圖,對于拋物線上任意一點D,都有DF=DH.
根據以上知識,我們來完成以下問題:
(1)因為拋物線是軸對稱圖形,由對稱性可知這個神奇的點F應在拋物線的 上,且準線l一定與對稱軸垂直即l⊥MN(對稱軸).
(2)若準線l與對稱軸MN交于E,MN交拋物線于點P,則PE、PF的數量關系是PE PF(填>、=、<),
(3)求拋物線y=﹣(x﹣2)2+4的神奇點(焦點)F的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是二次函數y=ax2+bx+c(a≠0)的圖象的一部分,給出下列命題:①a+b+c=0;②b>2a;③方程ax2+bx+c=0的兩根分別為﹣3和1;④當x<1時,y<0.其中正確的命題是( )
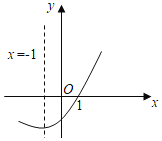
A.②③B.①③C.①②D.①③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某射擊隊教練為了了解隊員訓練情況,從隊員中選取甲、乙兩名隊員進行射擊測試,相同條件下各射靶5次,成績統計如下:
命中環數 | 6 | 7 | 8 | 9 | 10 |
甲命中相應環數的次數 | 0 | 1 | 3 | 1 | 0 |
乙命中相應環數的次數 | 2 | 0 | 0 | 2 | 1 |
(1)根據上述信息可知:甲命中環數的中位數是_____環,乙命中環數的眾數是______環;
(2)試通過計算說明甲、乙兩人的成績誰比較穩定?
(3)如果乙再射擊1次,命中8環,那么乙射擊成績的方差會變小.(填“變大”、“變小”或“不變”)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數y=ax2+bx+c(a≠0)的圖象的頂點在第一象限,且過點(0,1)和(﹣1,0).下列結論:①ab<0,②b2>4a,③0<a+b+c<2,④0<b<1,⑤當x>﹣1時,y>0,其中正確結論的個數是
A.5個 B.4個 C.3個 D.2個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,老張利用國慶假日在某釣魚場釣魚,風平浪靜時,魚漂露出水面部分AB=6m,微風吹來時,假設鉛錘P不動,魚漂移動了一段距離BC,且項場恰好與水面平齊(即PAPC,水平線1與OC夾角a=8°(點A在OC上,則鉛錘P處的水深h為( )(參考數據:sin8°=![]() ,cos8°=
,cos8°=![]() ,tan8°=
,tan8°=![]() )
)
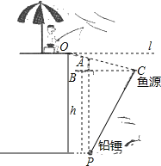
A.150cmB.144cmC.111cmD.105cm
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現代互聯網技術的廣泛應用,催生了快遞行業的高度發展.據調查,太原市某家小型“大學生自主創業”的快遞公司,今年九月份與十一月份完成投遞的快遞總件數分別為10萬件和12.1萬件.現假定該公司每月投遞的快遞總件數的增長率相同.
(1)求該快遞公司投遞總件數的月平均增長率;
(2)如果平均每人每月最多可投遞0.6萬件,那么該公司現有的21名快遞業務員能否完成今年十二月份的快遞投遞任務?如果不能,請問至少需要增加幾名業務員?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com