
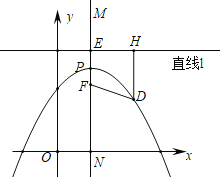
【題目】尋找神奇點!每條拋物線內都有一個神奇的點F(也叫焦點),還有一條與之配套的直線!(也叫準線),使得拋物線上的每個點到F的距離等于到直線l的距離.如圖,對于拋物線上任意一點D,都有DF=DH.
根據以上知識,我們來完成以下問題:
(1)因為拋物線是軸對稱圖形,由對稱性可知這個神奇的點F應在拋物線的 上,且準線l一定與對稱軸垂直即l⊥MN(對稱軸).
(2)若準線l與對稱軸MN交于E,MN交拋物線于點P,則PE、PF的數量關系是PE PF(填>、=、<),
(3)求拋物線y=﹣(x﹣2)2+4的神奇點(焦點)F的坐標.
【答案】(1)對稱軸;(2)=;(3)點F(2,![]() ).
).
【解析】
(1)拋物線是軸對稱圖形,則點F應該在拋物線的對稱軸上,即可求解;
(2)根據題意中焦點的性質解答即可;
(3)設PF=c,則點F的坐標和直線l的解析式可用含c的代數式表示,設D(m,![]() ),然后根據兩點間的距離公式分別表示出DF2和HD2,根據DF=DH,可得關于m、c的方程,解方程即可求出c,進而可得結果.
),然后根據兩點間的距離公式分別表示出DF2和HD2,根據DF=DH,可得關于m、c的方程,解方程即可求出c,進而可得結果.
解:(1)拋物線是軸對稱圖形,則點F應該在拋物線的對稱軸上,
故答案為:對稱軸;
(2)∵拋物線上的每個點到F的距離等于到直線l的距離,l⊥MN,∴PE=PF.
故答案為:=;
(3)如圖,設PF=c,頂點P(2,4),則點F(2,4﹣c),直線l:y=c+4,
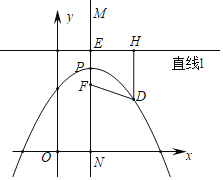
設D(m,![]() ),則DF2=
),則DF2=![]() =
=![]() ,
,
HD2=![]() ,
,
∵DF=DH,∴![]() =
=![]() ,
,
化簡得:1﹣2c=2c,解得:c=![]() ,
,
故點F(2,![]() ).
).


科目:初中數學 來源: 題型:
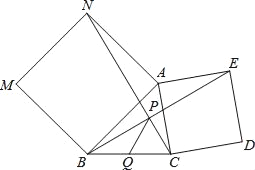
【題目】探究:如圖,分別以△ABC的兩邊AB和AC為邊向外作正方形ANMB和正方形ACDE,NC、BE交于點P.
求證:∠ANC=∠ABE.
應用:Q是線段BC的中點,若BC=6,則PQ= .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某游樂場試營業期間,每天運營成本為1000元.經統計發現,每天售出的門票張數![]() (張)與門票售價
(張)與門票售價![]() (元/張)之間滿足一次函數
(元/張)之間滿足一次函數![]() ,設游樂場每天的利潤為
,設游樂場每天的利潤為![]() (元).(利潤=票房收入-運營成本)
(元).(利潤=票房收入-運營成本)
(1)試求![]() 與
與![]() 之間的函數表達式.
之間的函數表達式.
(2)游樂場將門票售價定為多少元/張時,每天獲利最大?最大利潤是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,已知拋物線y=ax2+bx+c的圖像經過點A(0,3)、B(1,0),其對稱軸為直線l:x=2,過點A作AC∥x軸交拋物線于點C,∠AOB的平分線交線段AC于點E,點P是拋物線上的一個動點,設其橫坐標為m.

(1)求拋物線的解析式;
(2)若動點P在直線OE下方的拋物線上,連結PE、PO,當m為何值時,四邊形AOPE面積最大,并求出其最大值;
(3)如圖②,F是拋物線的對稱軸l上的一點,在拋物線上是否存在點P使△POF成為以點P為直角頂點的等腰直角三角形?若存在,直接寫出所有符合條件的點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,每次旋轉都以圖中的A、B、C、D、E、F中不同的點為旋轉中心,旋轉角度為k90°(k為整數),現在要將左邊的陰影四邊形正好通過n次旋轉得到右邊的陰影四邊形,則n的值可以是( )
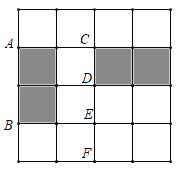
A.n=1可以,n=2,3不可B.n=2可以,n=1,3不可
C.n=1,2可以,n=3不可D.n=1,2,3均可
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,∠A=30°,AB=10,以AB為直徑的⊙O交BC于點D,交AC于點E,連接DE,過點B作BP平行于DE,交⊙O于點P,連接CP、OP.

(1)求證:點D為BC的中點;
(2)求AP的長度;
(3)求證:CP是⊙O的切線.
查看答案和解析>>
科目:初中數學 來源: 題型:
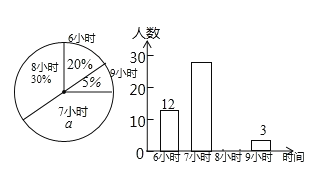
【題目】為了了解某校初中各年級學生每天的平均睡眠時間(單位:h,精確到1h),抽樣調查了部分學生,并用得到的數據繪制了下面兩幅不完整的統計圖.
請你根據圖中提供的信息,回答下列問題:
(1)求出扇形統計圖中百分數a的值為 ,所抽查的學生人數為 .
(2)求出平均睡眠時間為8小時的人數,并補全頻數直方圖.
(3)求出這部分學生的平均睡眠時間的眾數和平均數.
(4)如果該校共有學生1200名,請你估計睡眠不足(少于8小時)的學生數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c的圖象如圖,則下列敘述正確的是( )

A. abc<0 B. -3a+c<0
C. b2-4ac≥0 D. 將該函數圖象向左平移2個單位后所得到拋物線的解析式為y=ax2+c
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com