【題目】某社區調查社區居民雙休日的學習狀況，采取下列調查方式：①從一幢高層住宅樓中選取200名居民；②從不同住層樓中隨機選取200名居民；③選取社區內的200名在校學生．
（1）上述調查方式最合理的是 （填序號）；
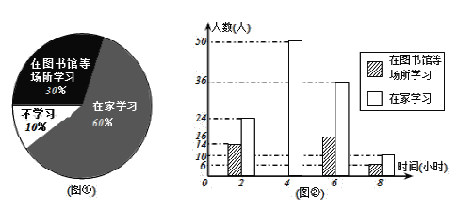
（2）將最合理的調查方式得到的數據制成扇形統計圖（如圖①）和頻數分布直方圖（如圖②）．
①請補全直方圖（直接畫在圖②中）；
②在這次調查中，200名居民中，在家學習的有 人；
（3）請估計該社區2000名居民中雙休日學習時間不少于4h的人數；
（4）小明的叔叔住在該社區，那么雙休日他去叔叔家時，正好叔叔沒有學習的概率是 ．
【答案】（1）②；（2）①見解析；②120；（3）1420人；（4）
【解析】
（1）抽樣調查時，為了獲得較為準確的調查結果，所以抽樣時要注意樣本的代表性和廣泛性；
（2）①先求出在圖書館等場所學習的總人數，再求出在圖書館等場所學習4小時的人數，然后補充統計圖即可；
②利用200名居民中，在家學習的占60%即可求出答案；
（3）首先利用頻數分布直方圖中的有關數據，計算出雙休日學習時間不少于4h的人數占樣本的百分比，然后利用樣本估計總體，即可算出該社區2000名居民中雙休日學習時間不少于4h的人數；
（4）從扇形統計圖中可以看出，不學習的占總體的百分比是10%，利用頻率來估計概率即可求出答案．
（1）抽樣調查時，為了獲得較為準確的調查結果，所以抽樣時要注意樣本的代表性和廣泛性，最合理的是②
（2）①200×30%-14-16-6=24，補充圖內形如下：
②200×60%=120；
（3）∵
=0.71，
∴2000×0.71=1420（人），
∴估計該社區2000名居民雙休日學習時間不少于4h的人數為1420人．
（4）從扇形統計圖中可以看出，不學習的占總體的百分比是10%，利用頻率來估計概率為．
閱讀快車系列答案科目：初中數學 來源： 題型：
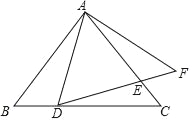
【題目】已知：如圖，在△ABC中，點D、E分別在邊BC、AC上，點F在DE的延長線上，AD＝AF，AECE＝DEEF．
（1）求證：△ADE∽△ACD；
（2）如果AEBD＝EFAF，求證：AB＝AC．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：如圖，在△ABC中，點D、E分別在邊BC和AB上，且AD＝AC，EB＝ED，分別延長ED、AC交于點F．
（1）求證：△ABD∽△FDC；
（2）求證：AE2＝BEEF．
查看答案和解析>>
科目：初中數學 來源： 題型：
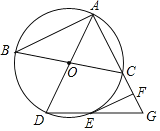
【題目】如圖，△ABC內接于⊙O，AD與BC是⊙O的直徑，延長線段AC至點G，使AG＝AD，連接DG交⊙O于點E，EF∥AB交AG于點F．
（1）求證：EF與⊙O相切．
（2）若EF＝2
，AC＝4，求扇形OAC的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在△ABC中，∠BAC＝90°，AB＝AC，AD⊥BC于點D．
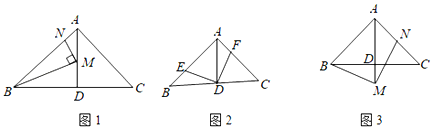
（1）如圖1，點M，N分別在AD，AB上，且∠BMN＝90°，當∠AMN＝30°，AB＝2時，求線段AM的長；
（2）如圖2，點E，F分別在AB，AC上，且∠EDF＝90°，求證：BE＝AF；
（3）如圖3，點M在AD的延長線上，點N在AC上，且∠BMN＝90°，求證：AB+AN＝
AM．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】二次函數y＝ax2＋bx＋c（a，b，c 為常數，且a≠0）的圖像上部分點的橫坐標x和縱
坐標y的對應值如下表
x | … | －1 | 0 | 1 | 2 | 3 | … |
y | … | －3 | －3 | －1 | 3 | 9 | … |
關于x的方程ax2＋bx＋c＝0一個負數解x1滿足k＜x1＜k+1（k為整數），則k＝________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】河南靈寶蘋果為中華蘋果之翹楚，被譽為“中華名果”．某水果超市計劃從靈寶購進“紅富士”與“新紅星”兩種品種的蘋果．已知2箱紅富士蘋果的進價與3箱新紅星蘋果的進價的和為282元，且每箱紅富士蘋果的進價比每箱新紅星蘋果的進價貴6元．
（1）求每箱紅富士蘋果的進價與每箱新紅星蘋果的進價分別是多少元？
（2）如果購進紅富士蘋果有優惠，優惠方案是：購進紅富士蘋果超過20箱，超出部分可以享受七折優惠．若購進
（
，且為整數）箱紅富士蘋果需要花費
元，求與之間的函數關系式；
（3）在（2）的條件下，超市決定在紅富士、新紅星兩種蘋果中選購其中一種，且數量超過20箱，請你幫助超市選擇購進哪種蘋果更省錢．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
