
【題目】如圖,把△EFP放置在菱形ABCD中,使得頂點E,F,P分別在線段AB,AD,AC上,已知EP=FP=6,EF=![]() ,∠BAD=60°,且AB>
,∠BAD=60°,且AB>![]() .
.
(1)求∠EPF的大小;
(2)若AP=10,求AE+AF的值;
(3)若△EFP的三個頂點E、F、P分別在線段AB、AD、AC上運動,請直接寫出AP長的最大值和最小值.
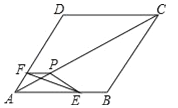
【答案】(1)120°;(2)![]() ;(3)AP的最大值為12,AP的最小值為6.
;(3)AP的最大值為12,AP的最小值為6.
【解析】
試題分析:(1)根據銳角三角函數求出∠FPG,最后求出∠EPF.
(2)先判斷出Rt△PME≌Rt△PNF,再根據銳角三角函數求解即可,(3)根據運動情況及菱形的性質判斷求出AP最大和最小值.
試題解析:(1)過點P作PG⊥EF于點G,如圖1所示.
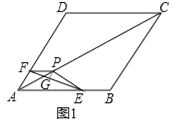
∵PE=PF=6,EF![]() ,∴FG=EG=
,∴FG=EG=![]() ,∠FPG=∠EPG=
,∠FPG=∠EPG=![]() ∠EPF.
∠EPF.
在Rt△FPG中,sin∠FPG=![]() =
=![]() =
=![]() ,∴∠FPG=60°,∴∠EPF=120°;
,∴∠FPG=60°,∴∠EPF=120°;
(2)過點P作PM⊥AB于點M,作PN⊥AD于點N,如圖2所示.
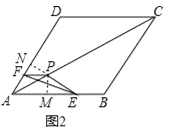
∵AC為菱形ABCD的對角線,∴∠DAC=∠BAC,AM=AN,PM=PN.
在Rt△PME和Rt△PNF中,PM=PN,PE=PF,∴Rt△PME≌Rt△PNF,∴ME=NF.
又AP=10,∠PAM=![]() ∠DAB=30°,∴AM=AN=APcos30°=10×
∠DAB=30°,∴AM=AN=APcos30°=10×![]() =
=![]() ,∴AE+AF=(AM+ME)+(AN﹣NF)=AM+AN=
,∴AE+AF=(AM+ME)+(AN﹣NF)=AM+AN=![]() ;
;
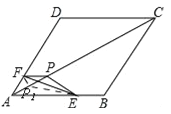
(3)如圖,當△EFP的三個頂點分別在AB,AD,AC上運動,點P在P1,P之間運動,∴P1O=PO=3,AO=9,∴AP的最大值為12,AP的最小值為6.


 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,過點B(6,0)的直線AB與直線OA相交于點A(4,2),動點M沿路線O→A→C運動. 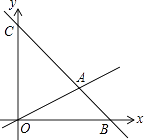
(1)求直線AB的解析式.
(2)求△OAC的面積.
(3)當△OMC的面積是△OAC的面積的 ![]() 時,求出這時點M的坐標.
時,求出這時點M的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在正方形ABCD中,點E,F分別在邊BC,CD上,且∠EAF=∠CEF=45°.
(1)將△ADF繞著點A順時針旋轉90°,得到△ABG(如圖①),求證:△AEG≌△AEF;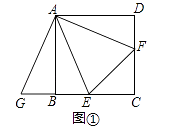
(2)若直線EF與AB,AD的延長線分別交于點M,N(如圖②),求證:EF2=ME2+NF2;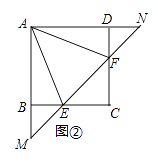
(3)將正方形改為長與寬不相等的矩形,若其余條件不變(如圖③),請你直接寫出線段EF,BE,DF之間的數量關系.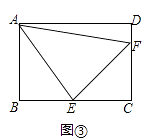
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com