Question

19．如圖，正方形ABCD的邊長為4，動點M、N同時從A點出發，點M沿AB以每秒1個單位長度的速度向中點B運動，點N沿折現ADC以每秒2個單位長度的速度向終點C運動，設運動時間為t秒，則△CMN的面積為S關于t函數的圖象大致是（　　）

• A．
• B．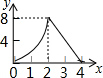
• C．
• D．

Answer 1

分析 當0≤t≤2時，AM=t，AN=2t，利用S=S_{正方形ABCD}-S_△AMN-S_△BCM-S_△CDN可得到S=-t²+6t；當2＜t≤4時，CN=8-2t，利用三角形面積公式可得S=-4t+16，于是可判斷當0≤t≤2時，S關于t函數的圖象為開口向上的拋物線的一部分，當2＜t≤4時，S關于t函數的圖象為一次函數圖象的一部分，然后利用此特征對四個選項進行判斷．

解答 解：當0≤t≤2時，AM=t，AN=2t，
所以S=S_{正方形ABCD}-S_△AMN-S_△BCM-S_△CDN=4×4-$\frac{1}{2}$•t•2t-$\frac{1}{2}$•4•（4-t）-$\frac{1}{2}$•4•（4-2t）=-t²+6t；
當2＜t≤4時，CN=8-2t，S=$\frac{1}{2}$•（8-2t）•4=-4t+16，
即當0≤t≤2時，S關于t函數的圖象為開口向下的拋物線的一部分，當2＜t≤4時，S關于t函數的圖象為一次函數圖象的一部分．
故選D．

點評 本題考查了動點問題的函數圖象：函數圖象是典型的數形結合，圖象應用信息廣泛，通過看圖獲取信息，不僅可以解決生活中的實際問題，還可以提高分析問題、解決問題的能力．解決本題的關鍵是利用分類討論的思想求出S與t的函數關系式．