
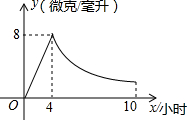
 某藥品研究所開發一種抗菌新藥,經多年動物實驗,首次用于臨床人體試驗,測得成人服藥后血液中藥物濃度y(微克/毫升)與服藥時間x小時之間函數關系如圖所示(當4≤x≤10時,y與x成反比例).
某藥品研究所開發一種抗菌新藥,經多年動物實驗,首次用于臨床人體試驗,測得成人服藥后血液中藥物濃度y(微克/毫升)與服藥時間x小時之間函數關系如圖所示(當4≤x≤10時,y與x成反比例).分析 (1)當0≤x≤4時,設直線解析式為:y=kx,當4≤x≤10時,設反比例函數解析式為:y=$\frac{a}{x}$,利用待定系數法即可解決問題.
(2)分別求出y=2時的兩個函數值,再求時間差即可解決問題.
解答 解:(1)當0≤x≤4時,設直線解析式為:y=kx,將(4,8)代入得:8=4k,
解得:k=2,故直線解析式為:y=2x,…(2分)
當4≤x≤10時,設反比例函數解析式為:y=$\frac{a}{x}$,將(4,8)代入得:8=$\frac{a}{4}$,
解得:a=32,故反比例函數解析式為:y=$\frac{32}{x}$;
因此血液中藥物濃度上升階段的函數關系式為y=2x(0≤x≤4),
下降階段的函數關系式為y=$\frac{32}{x}$(4≤x≤10).
(2)當y=2,則2=2x,解得:x=1,
當y=2,則2=$\frac{32}{x}$,解得:x=16,
∵16-1=15(小時),
∴血液中藥物濃度不低于2微克/毫升的持續時間15小時.
點評 本題考查一次函數的應用、反比例函數的應用等知識,解題的關鍵是靈活應用待定系數法解決問題,學會利用函數圖象解決實際問題,屬于中考常考題型.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 測量體校籃球隊和排球隊中180名隊員的身高 | |
| B. | 隨機抽取本市一所學校的180名學生的身高 | |
| C. | 查閱有關外地180名學生身高的統計資料 | |
| D. | 在本地的市區和郊縣各任選一所完全中學、兩所初級中學,在這六所學校的七、八、九年級的一個班中,用抽簽的方法分別選出10名學生,然后測量他們的身高. |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com