综合中文字幕,亚州精品国产,亚洲综合在线视频

精英家教網 > 初中數學 > 題目詳情

【題目】如圖,在平面直角坐標系中,已知三個頂點的坐標分別是.

(1)請在圖中,畫出繞著點逆時針旋轉后得到的,則的正切值為 .

(2)以點為位似中心,將縮小為原來的,得到,請在圖中軸左側,畫出,若點是上的任意一點,則變換后的對應點的坐標是 .

【答案】（1）圖詳見解析，；（2）圖詳見解析，變換后的對應點的坐標是.

【解析】

1）依據旋轉的方向、角度和旋轉中心，即可得到△ABC繞著點O逆時針旋轉90°后得到的△A1B1C1，進而得到∠A1C1B1的正切值；.

（2）依據點O為位似中心，將△ABC縮小為原來的，即可得到△A2B2C2，以及變換后的對應點P′的坐標．

(1)如圖所示,即為所求；由題可得，；

(2)如圖所示,即為所求，

∵點是上的任意一點，點為位似中心，

∴變換后的對應點的坐標是.

練習冊系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：初中數學 來源： 題型：

【題目】某校文體藝術節期間，舉辦“愛我云南，唱我云南”文藝晚會．每個班推薦一個節目參加晩會表演，參加晚會表演的節目均獲獎，獎項分為一等獎、二等獎、三等獎和優秀獎，明明根據獲獎情況繪制岀如圖所示的兩幅統計圖．請你根據圖中所給信息解答下列問題．

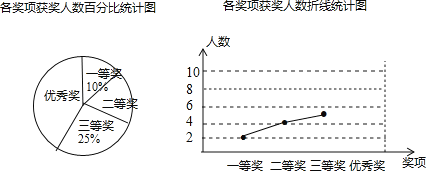
（1）二等獎的獲獎人數所占的百分比是　；

（2）在此次比賽中，一共有多少同學參賽？請將折線統計圖補充完整．

查看答案和解析>>

科目：初中數學 來源： 題型：

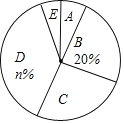
【題目】某校為了解全校學生對新聞、體育、動畫、娛樂、戲曲五類電視節目的喜愛情況，隨機選取該校部分學生進行調查，要求每名學生從中只選一類最喜愛的電視節目，以下是根據調查結果繪制的統計圖表的一部分．

類別	A	B	C	D	E
節目類型	新聞	體育	動畫	娛樂	戲曲
人數	12	30	m	54	9

請你根據以上的信息，回答下列問題：

（1）被調查的學生中，最喜愛體育節目的有　　人，這些學生數占被調查總人數的百分比為　　%．

（2）被調查學生的總數為　　人，統計表中m的值為　　，統計圖中n的值為　　．

（3）在統計圖中，E類所對應扇形圓心角的度數為　　．

（4）該校共有2000名學生，根據調查結果，估計該校最喜愛新聞節目的學生數．

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】數軸上的A、B、C三點所表示的數分別為a、b、1，且|a﹣1|+|b﹣1|＝|a﹣b|，則下列選項中，滿足A、B、C三點位置關系的數軸為（　　）

A. B.

C. D.

查看答案和解析>>

科目：初中數學 來源： 題型：

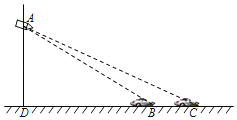
【題目】如圖，一輛轎車在經過某路口的感應線B和C處時，懸臂燈桿上的電子警察拍攝到兩張照片，兩感應線之間距離BC為6m，在感應線B、C兩處測得電子警察A的仰角分別為∠ABD＝18°，∠ACD＝14°．求電子警察安裝在懸臂燈桿上的高度AD的長．

（參考數據：sin14°≈0.242，cos14°≈0.97，tan14°≈0.25，sin18°≈0.309，cos18°≈0.951，tan18°≈0.325）

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】（問題引入）

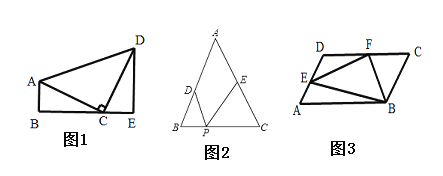
如圖（1），在中，，，過作則交延長線于點，則易得

（直接應用）

如圖,已知等邊的邊長為,點, 分別在邊, 上, , 為中點，為當上一動點，當在何處時，與相似，求的值.

（拓展應用）

已知在平行四邊形中，，，，,，求長.

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】聯想三角形外心的概念，我們可引入如下概念。

定義：到三角形的兩個頂點距離相等的點，叫做此三角形的準外心。

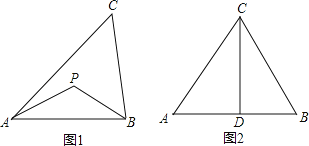
舉例：如圖1，若PA=PB，則點P為△ABC的準外心。

應用：如圖2，CD為等邊三角形ABC的高，準外心P在高CD上，且PD=AB，求∠APB的度數。

探究：已知△ABC為直角三角形，斜邊BC=5，AB=3，準外心P在AC邊上，試探究PA的長。

查看答案和解析>>

科目：初中數學 來源： 題型：

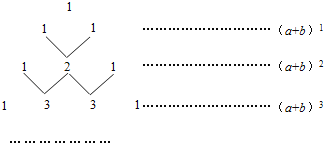
【題目】我國古代數學的許多發現都曾位居世界前列，其中“楊輝三角”就是一例．如圖，這個三角形的構造法則：兩腰上的數都是1，其余每個數均為其上方左、右兩數之和，它給出了（a+b）n（n為正整數）的展開式（按a的次數由大到小的順序排列）的系數規律．例如，在三角形中第三行的三個數1，2，1，恰好對應（a+b）2＝a2+2ab+b2展開式中的系數；第四行的四個數1，3，3，1，恰好對應著（a+b）3＝a3+3a2b+3ab2+b2展開式中的系數等．

（1）（a+b）n展開式中項數共有　　項．

（2）寫出（a+b）5的展開式：（a+b）5＝　　．

（3）利用上面的規律計算：25﹣5×24+10×23﹣10×22+5×2﹣1．

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】如圖，在平面直角坐標系中，△ABC的頂點坐標為A（﹣2，3），B（﹣3，2），C（﹣1，1）．

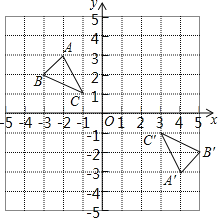
（1）若將△ABC向右平移3個單位長度，再向上平移1個單位長度，請畫出平移后的△A1B1C1；

（2）畫出△A1B1C1繞原點順時針旋90°后得到的△A2B2C2；

（3）若△A′B′C′與△ABC是中心對稱圖形，則對稱中心的坐標為．

查看答案和解析>>

同步練習冊答案

日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

練習冊

高中

初中

小學