
【題目】小明,小亮都想去觀看電影,但是只有一張電影票,他們決定采取抽卡片的辦法確定誰去,規(guī)定如下:將正面分別標有數(shù)字![]() ,
,![]() ,
,![]() 的三張卡片(除數(shù)字外其余都同)洗勻后背面朝上放置在桌面上,隨機抽出一張記下數(shù)字后放回,重新洗勻后背面朝上放置在桌面上,再隨機抽出一張記下數(shù)字,如果兩個數(shù)字的積為奇數(shù),則小明去;如果兩個數(shù)字的積為偶數(shù),則小亮去.
的三張卡片(除數(shù)字外其余都同)洗勻后背面朝上放置在桌面上,隨機抽出一張記下數(shù)字后放回,重新洗勻后背面朝上放置在桌面上,再隨機抽出一張記下數(shù)字,如果兩個數(shù)字的積為奇數(shù),則小明去;如果兩個數(shù)字的積為偶數(shù),則小亮去.
(1)請用列表或樹狀圖的方法表示抽出的兩張卡片上的數(shù)字積的所有可能出現(xiàn)的結(jié)果;
(2)你認為這個規(guī)則公平嗎?請說明理由.
【答案】(1)見詳解;(2)游戲不公平,理由見詳解;
【解析】
(1)根據(jù)題意直接列表或畫樹狀圖即可;
(2)先分別求出兩紙牌上的數(shù)字之積的所有情況,再求出其中偶數(shù)和奇數(shù)的個數(shù),即可求出小明獲勝的概率和小亮獲勝的概率,最后得出游戲是否公平.
(1)畫樹狀圖如圖:
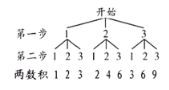
(2)由(1)知一共有![]() 種等可能情形,其中出現(xiàn)積為奇數(shù)的情況有
種等可能情形,其中出現(xiàn)積為奇數(shù)的情況有![]() 種,出現(xiàn)積為偶數(shù)的情況有
種,出現(xiàn)積為偶數(shù)的情況有![]() 種,則
種,則![]() (數(shù)字之積為奇數(shù))
(數(shù)字之積為奇數(shù))![]() ,
,![]() (數(shù)字之積為偶數(shù))
(數(shù)字之積為偶數(shù))![]()
![]() (數(shù)字之積為奇數(shù))
(數(shù)字之積為奇數(shù))![]()
![]() (數(shù)字之積為偶數(shù)),
(數(shù)字之積為偶數(shù)),
所以游戲不公平.


科目:初中數(shù)學 來源: 題型:
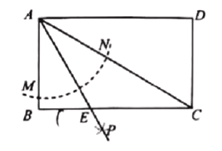
【題目】如圖,矩形![]() 以點
以點![]() 為圓心,以任意長為半徑作弧分別交
為圓心,以任意長為半徑作弧分別交![]() 、
、![]() 于
于![]() 兩點,再分別以點
兩點,再分別以點![]() 為圓心,以大于
為圓心,以大于![]() 的長為半徑作弧交于點
的長為半徑作弧交于點![]() ,作射線
,作射線![]() 交
交![]() 于點
于點![]() ,若
,若![]() ,則矩形
,則矩形![]() 的面積等于__________.
的面積等于__________.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】定義:我們知道,四邊形的一條對角線把這個四邊形分成了兩個三角形,如果這兩個三角形相似(不全等),我們就把這條對角線叫做這個四邊形的“相似對角線”.
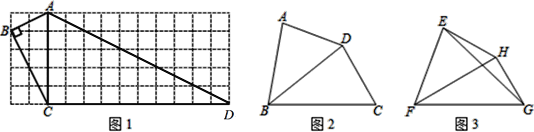
(1)如圖1,已知四邊形![]() 在正方形網(wǎng)格中,頂點都在格點上,判斷:四邊形
在正方形網(wǎng)格中,頂點都在格點上,判斷:四邊形![]() ______(填“是”或“不是”)以
______(填“是”或“不是”)以![]() 為“相似對角線”的四邊形;
為“相似對角線”的四邊形;
(2)如圖![]() ,在四邊形
,在四邊形![]() 中,
中,![]() ,
,![]() ,對角線
,對角線![]() 平分
平分![]() .求證:
.求證:![]() 是四邊形
是四邊形![]() 的“相似對角線”;
的“相似對角線”;
(3)如圖![]() ,已知
,已知![]() 是四邊形
是四邊形![]() 的“相似對角線”,
的“相似對角線”,![]() .連接
.連接![]() ,若
,若![]() 的面積為
的面積為![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在等腰![]() ABC中,AB=AC,∠BAC=50°,∠BAC的平分線與AB的垂直平分線交于點O、點C沿EF折疊后與點O重合,則∠CEF的度數(shù)是( )
ABC中,AB=AC,∠BAC=50°,∠BAC的平分線與AB的垂直平分線交于點O、點C沿EF折疊后與點O重合,則∠CEF的度數(shù)是( )
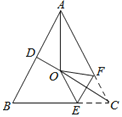
A. 60° B. 55° C. 50° D. 45°
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
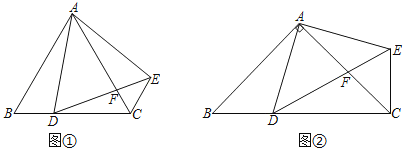
【題目】如圖①,在△ABC中,AB=AC,∠BAC=60°,D為BC邊上一點(不與點B,C重合),將線段AD繞點A逆時針旋轉(zhuǎn)60°得到AE,連接EC,則:
(1)①∠ACE的度數(shù)是 ; ②線段AC,CD,CE之間的數(shù)量關(guān)系是 .
(2)如圖②,在△ABC中,AB=AC,∠BAC=90°,D為BC邊上一點(不與點B,C重合),將線段AD繞點A逆時針旋轉(zhuǎn)90°得到AE,連接EC,請判斷線段AC,CD,CE之間的數(shù)量關(guān)系,并說明理由;
(3)如圖②,AC與DE交于點F,在(2)條件下,若AC=8,求AF的最小值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖, 已知二次函數(shù)![]() (
(![]() ,
,![]() ,
,![]() 為常數(shù))的對稱軸為
為常數(shù))的對稱軸為![]() ,與
,與![]() 軸的交點為
軸的交點為![]() ,
,![]() 的最大值為5,頂點為
的最大值為5,頂點為![]() ,過點
,過點![]() 且平行于
且平行于![]() 軸的直線與拋物線交于點
軸的直線與拋物線交于點![]() ,
,![]() .
.

(1)求該二次函數(shù)的解析式和點![]() ,
,![]() 的坐標.
的坐標.
(2)點![]() 是直線
是直線![]() 上的動點,若點
上的動點,若點![]() ,點
,點![]() ,點
,點![]() 所構(gòu)成的三角形與
所構(gòu)成的三角形與![]() 相似,求出所有點
相似,求出所有點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
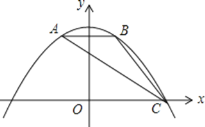
【題目】如圖,拋物線![]() 經(jīng)過
經(jīng)過![]() 的三個頂點,與
的三個頂點,與![]() 軸相交于
軸相交于![]() ,點
,點![]() 坐標為
坐標為![]() ,點
,點![]() 是點
是點![]() 關(guān)于
關(guān)于![]() 軸的對稱點,點
軸的對稱點,點![]() 在
在![]() 軸的正半軸上.
軸的正半軸上.
(1)求該拋物線的函數(shù)解析式;
(2)點![]() 為線段
為線段![]() 上一動點,過點
上一動點,過點![]() 作
作![]() 軸,
軸,![]() 軸, 垂足分別為點
軸, 垂足分別為點![]() ,
,![]() ,當四邊形
,當四邊形![]() 為正方形時,求出點
為正方形時,求出點![]() 的坐標;
的坐標;
(3)將(2) 中的正方形![]() 沿
沿![]() 向右平移,記平移中的正方形
向右平移,記平移中的正方形![]() 為正方形
為正方形![]() ,當點
,當點![]() 和點
和點![]() 重合時停止運動, 設(shè)平移的距離為
重合時停止運動, 設(shè)平移的距離為![]() ,正方形的邊
,正方形的邊![]() 與
與![]() 交于點
交于點![]() ,
,![]() 所在的直線與
所在的直線與![]() 交于點
交于點![]() , 連接
, 連接![]() ,是否存在這樣的
,是否存在這樣的![]() ,使
,使![]() 是等腰三角形?若存在,求
是等腰三角形?若存在,求![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com