
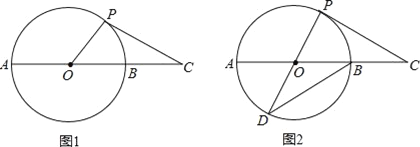
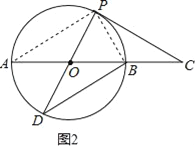
【題目】如圖1,延長⊙O的直徑AB至點C,使得BC=![]() AB,點P是⊙O上半部分的一個動點(點P不與A、B重合),連結OP,CP.
AB,點P是⊙O上半部分的一個動點(點P不與A、B重合),連結OP,CP.
(1)∠C的最大度數為 ;
(2)當⊙O的半徑為3時,△OPC的面積有沒有最大值?若有,說明原因并求出最大值;若沒有,請說明理由;
(3)如圖2,延長PO交⊙O于點D,連結DB,當CP=DB時,求證:CP是⊙O的切線.
【答案】(1)30°;(2)有最大值為9,理由見解析;(3)證明見解析.
【解析】試題分析:(1)當PC與⊙O相切時,∠OCP的度數最大,根據切線的性質即可求得;
(2)由△OPC的邊OC是定值,得到當OC邊上的高為最大值時,△OPC的面積最大,當PO⊥OC時,取得最大值,即此時OC邊上的高最大,于是得到結論;
(3)根據全等三角形的性質得到AP=DB,根據等腰三角形的性質得到∠A=∠C,得到CO=OB+OB=AB,推出△APB≌△CPO,根據全等三角形的性質得到∠CPO=∠APB,根據圓周角定理得到∠APB=90°,即可得到結論.
試題解析:(1)當PC與⊙O相切時,∠OCP最大.如圖1,所示:
∵sin∠OCP=![]() =
=![]() =
=![]() ,∴∠OCP=30°
,∴∠OCP=30°
∴∠OCP的最大度數為30°,
故答案為:30°;
(2)有最大值,理由:
∵△OPC的邊OC是定值,∴當OC邊上的高為最大值時,△OPC的面積最大,
而點P在⊙O上半圓上運動,當PO⊥OC時,取得最大值,即此時OC邊上的高最大,
也就是高為半徑長,∴最大值S△OPC=![]() OCOP=
OCOP=![]() ×6×3=9;
×6×3=9;
(3)連結AP,BP,如圖2,
在△OAP與△OBD中, 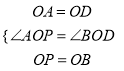 ,∴△OAP≌△OBD,∴AP=DB,
,∴△OAP≌△OBD,∴AP=DB,
∵PC=DB,∴AP=PC,
∵PA=PC,∴∠A=∠C,
∵BC=![]() AB=OB,∴CO=OB+OB=AB,
AB=OB,∴CO=OB+OB=AB,
在△APB和△CPO中, 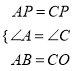 ,∴△APB≌△CPO,∴∠CPO=∠APB,
,∴△APB≌△CPO,∴∠CPO=∠APB,
∵AB為直徑,∴∠APB=90°,∴∠CPO=90°,
∴PC切⊙O于點P,即CP是⊙O的切線.


 期末1卷素質教育評估卷系列答案
期末1卷素質教育評估卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,AC=BC,AB=8,點D為AB的中點,若直角MDN繞點D旋轉,分別交AC于點E,交BC于點F,則下列說法正確的有( )
①AE=CF;②EC+CF=![]() ;③DE=DF;
;③DE=DF;
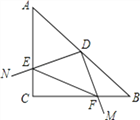
A. ①② B. ①③ C. ①②③ D. ①
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠BAC=90°,AB=AC.
(1)利用尺規,以AB為直徑作⊙O,交BC于點D;(保留作圖痕跡,不寫作法)
(2)在(1)所作的圖形中,求證:AC2=CDCB.

查看答案和解析>>
科目:初中數學 來源: 題型:
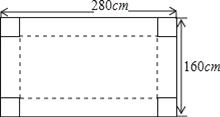
【題目】我國水資源比較缺乏,人均水量約為世界人均水量的四分之一,其中西北地區缺水尤為嚴重.一村民為了蓄水,他把一塊矩形白鐵皮四個角各切去一個同樣大小的小正方形后制作一個無蓋水箱用于接雨水.已知白鐵皮的長為280cm,寬為160cm(如圖).
(1)若水箱的底面積為16000cm2,請求出切去的小正方形邊長;
(2)對(1)中的水箱,若盛滿水,這時水量是多少升?(注:1升水=1000cm3水)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校要從小王和小李兩名同學中挑選一人參加全市知識競賽,在最近的五次選拔測試中,他倆的成績分別如下表:
次數 | 1 | 2 | 3 | 4 | 5 |
小王 | 60 | 75 | 100 | 90 | 75 |
小李 | 70 | 90 | 100 | 80 | 80 |
根據上表解答下列問題:
(1)完成下表:
姓名 | 平均成績(分) | 中位數(分) | 眾數(分) | 方差 |
小王 | 80 | 75 | 75 | 190 |
小李 |
(2)在這五次測試中,成績比較穩定的同學是誰?若將80分以上(含80分)的成績視為優秀,則小王、小李在這五次測試中的優秀率各是多少?
(3)歷屆比賽表明,成績達到80分以上(含80分)就很可能獲獎,成績達到90分以上(含90分)就很可能獲得一等獎,那么你認為選誰參加比賽比較合適?說明你的理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列下列命題是真命題的是( )
A. 過一點有且只有一條直線與已知直線垂直
B. 相等的兩個角一定是對頂角
C. 將一根細木條固定在墻上,只需要一根釘子
D. 同角的余角相等
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC是直角三角形,延長AB到點E,使BE=BC,在BC上取一點F,使BF=AB,連接EF,△ABC旋轉后能與△FBE重合,請回答:
(1)旋轉中心是點______,旋轉的最小角度是______度
(2)AC與EF的位置關系如何,并說明理由。

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com