【答案】
分析:(1)提取二次項系數3,然后根據完全平方公式配成平方的形式,再求解即可;
(2)把括號內的分式相加,除式的分母分解因式并把除法轉化為乘法,然后進行計算即可得解;
(3)先求出兩個不等式的解集,再求其公共解;
(4)把第二個方程整理成y=x-4,然后利用代入消元法求解即可.
解答:解:(1)移項得,3x
2-6x=1,
配方得,3x
2-6x+3=1+3,
即3(x-1)
2=4,
(x-1)
2=

,
開方得,x-1=±
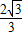
,
x
1=1+
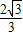
,x
2=1-
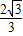
;
(2)(1+
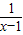
)÷
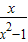
,
=
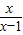
•
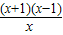
,
=x+1;
(3)
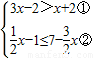
,
由①得,x>2,
由②得,x≤4,
所以,不等式組的解集是2<x≤4;
(4)
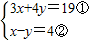
,
由②得,y=x-4③,
③代入①得,3x+4(x-4)=19,
解得x=5,
把x=5代入③得,y=5-4=1,
所以,方程組的解是

.
點評:(1)考查了用配方法解一元二次方程的步驟:
①形如x
2+px+q=0型:第一步移項,把常數項移到右邊;第二步配方,左右兩邊加上一次項系數一半的平方;第三步左邊寫成完全平方式;第四步,直接開方即可.
②形如ax
2+bx+c=0型,方程兩邊同時除以二次項系數,即化成x
2+px+q=0,然后配方;
(2)考查了分式的混合運算,準確分解因式是解題的關鍵;
(3)主要考查了一元一次不等式組解集的求法,其簡便求法就是用口訣求解.求不等式組解集的口訣:同大取大,同小取小,大小小大中間找,大大小小找不到(無解);
(4)考查的是二元一次方程組的解法,方程組中未知數的系數較小時可用代入法,當未知數的系數相等或互為相反數時用加減消元法較簡單.

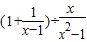 ;
;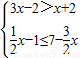 ;
;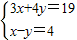 .
. ,
,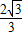 ,
,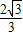 ,x2=1-
,x2=1-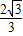 ;
;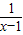 )÷
)÷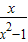 ,
,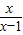 •
•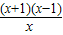 ,
,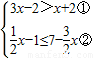 ,
,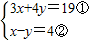 ,
, .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案