
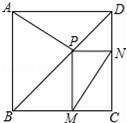
如圖,點(diǎn)P是正方形ABCD的對(duì)角線BD上的一點(diǎn),PM⊥BC,PN⊥CD,垂足分別為點(diǎn)M,N.求證:AP=MN.

【考點(diǎn)】全等三角形的判定與性質(zhì);矩形的判定與性質(zhì);正方形的性質(zhì).
【專(zhuān)題】證明題.
【分析】連接PC,根據(jù)正方形的性質(zhì)可得∠BCD=90°,∠ABD=∠CBD=45°,AB=BC,然后求出四邊形PMCN是矩形,根據(jù)矩形的對(duì)角線相等可得PC=MN,再利用“邊角邊”證明△ABP和△CBP全等,根據(jù)全等三角形對(duì)應(yīng)邊相等可得AP=PC,從而得解.
【解答】解:連接PC,
∵四邊形ABCD為正方形,
∴∠BCD=90°,∠ABD=∠CBD=45°,AB=BC,
又∵PN⊥DC,PM⊥BC,
∴∠PMC=90°,∠PNC=90°,
∴四邊形PMCN為矩形,
∴PC=MN,
在△ABP和△CBP中,

 ,
,
∴△ABP≌△CBP(SAS),
∴AP=PC,
∴AP=MN.

【點(diǎn)評(píng)】本題考查了正方形的性質(zhì),全等三角形的判定與性質(zhì),矩形的判定與性質(zhì),作出輔助線,構(gòu)造出全等三角形是解題的關(guān)鍵.


 芝麻開(kāi)花課程新體驗(yàn)系列答案
芝麻開(kāi)花課程新體驗(yàn)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
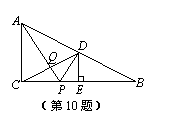
如圖,在Rt△ABC中,∠ACB=90°,點(diǎn)D是AB邊的中點(diǎn),過(guò)D作DE⊥BC于點(diǎn)E,點(diǎn)P是邊BC上的一個(gè)動(dòng)點(diǎn),AP與CD相交于點(diǎn)Q.當(dāng)AP+PD的值最小時(shí),AQ與PQ之間的數(shù)量關(guān)系是………………………………………………………………( )
 A.AQ=
A.AQ= 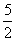 PQ B.AQ=3PQ C.AQ=
PQ B.AQ=3PQ C.AQ= 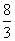 PQ D.AQ=4PQ
PQ D.AQ=4PQ
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
.如圖,直線CD與直線AB相交于C,根據(jù)下列語(yǔ)句畫(huà)圖
(1)過(guò)點(diǎn)P作PQ∥CD,交AB于點(diǎn)Q;
(2)過(guò)點(diǎn)P作PR⊥CD,垂足為R;
(3)若∠DCB=120°,猜想∠PQC是多少度?并說(shuō)明理由.


查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
已知:如圖,AB⊥CD,垂足為O,EF為過(guò)點(diǎn)O的一條直線,則∠1與∠2的關(guān)系一定成立的是( )


A.相等 B.互余 C.互補(bǔ) D.互為對(duì)頂角
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
在平面直角坐標(biāo)系中,將三角形各點(diǎn)的橫坐標(biāo)都減去3,縱坐標(biāo)保持不變,所得圖形與原圖形相比( )
A.向右平移了3個(gè)單位 B.向左平移了3個(gè)單位
C.向上平移了3個(gè)單位 D.向下平移了3個(gè)單位
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
已知,如圖,正方形ABCD,菱形EFGP,點(diǎn)E、F、G分別在AB、AD、CD上,延長(zhǎng)DC,PH⊥DC于H.
(1)求證:GH=AE;
(2)若菱形EFGP的周長(zhǎng)為20cm,
 ,F(xiàn)D=2,求△PGC的面積.
,F(xiàn)D=2,求△PGC的面積.


查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
把一塊直尺與一塊三角板如圖放置,若∠1=40°,則∠2的度數(shù)為( )


A.125° B.120° C.140° D.130°
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com