
已知⊙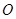 的半徑為1,以
的半徑為1,以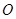 為原點,建立如圖所示的直角坐標系.有一個正方形
為原點,建立如圖所示的直角坐標系.有一個正方形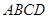 ,頂點
,頂點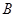 的坐標為(
的坐標為(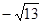 ,0),頂點
,0),頂點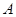 在
在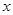 軸上方,頂點
軸上方,頂點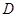 在⊙
在⊙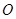 上運動.
上運動.
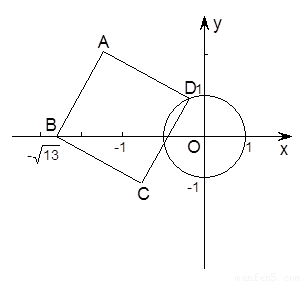
(1)當點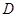 運動到與點
運動到與點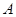 、
、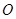 在一條直線上時,
在一條直線上時,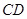 與⊙
與⊙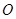 相切嗎?如果相切,請說明理由,并求出
相切嗎?如果相切,請說明理由,并求出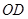 所在直線對應的函數表達式;如果不相切,也請說明理由;
所在直線對應的函數表達式;如果不相切,也請說明理由;
(2)設點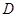 的橫坐標為
的橫坐標為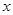 ,正方形
,正方形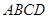 的面積為
的面積為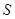 ,求出
,求出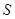 與
與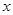 的函數關系式,并求出
的函數關系式,并求出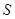 的最大值和最小值.
的最大值和最小值.
(1)CD與⊙O相切,y=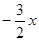 (2)S
(2)S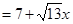 ,S的最大值為
,S的最大值為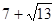 ,S的最小值為
,S的最小值為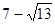
【解析】(1)CD與⊙O相切。 1分
因為A、D、O在一直線上,∠ADC=90°,
所以∠COD=90°,所以CD是⊙O的切線 3分
CD與⊙O相切時,有兩種情況:①切點在第二象限時(如圖①),
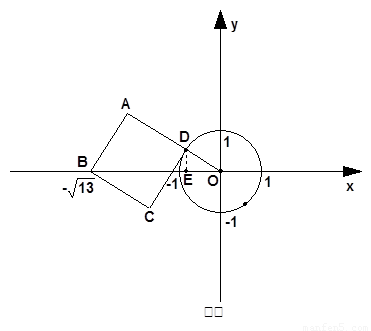
設正方形ABCD的邊長為a,則a2+(a+1)2=13,
解得a=2,或a=-3(舍去) 4分
過點D作DE⊥OB于E,則Rt△ODE≌Rt△OBA,所以 ,所以DE=
,所以DE=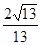 ,
,
OE= ,所以點D1的坐標是(-
,所以點D1的坐標是(- ,
,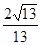 )
5分
)
5分
所以OD所在直線對應的函數表達式為y=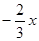 6分
6分
②切點在第四象限時(如圖②),
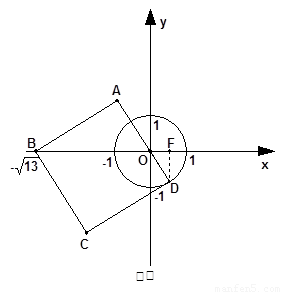
設正方形ABCD的邊長為b,則b2+(b-1)2=13,
解得b=-2(舍去),或b=3 7分
過點D作DF⊥OB于F,則Rt△ODF∽Rt△OBA,所以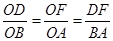 ,所以OF=
,所以OF=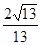 ,DF=
,DF= ,所以點D2的坐標是(
,所以點D2的坐標是(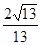 ,-
,- )
8分
)
8分
所以OD所在直線對應的函數表達式為y=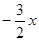 9分
9分
(2)如圖③,
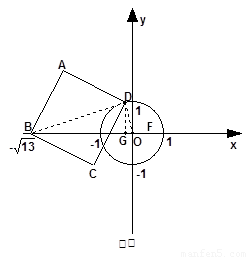
過點D作DG⊥OB于G,連接BD、OD,則BD2=BG2+DG2=(BO-OG)2+OD2-OG2=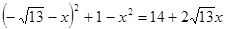 10分
10分
所以S=AB2=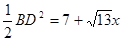 11分
11分
因為-1≤x≤1,所以S的最大值為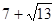 ,
,
S的最小值為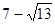 12分
12分
(1)易證CD是⊙O的切線,根據Rt△ODE∽Rt△OBA得到DE的長,再求出D1的坐標,根據待定系數法,求出函數解析式;
(2)過點D作DG⊥OB于G,連接BD、OD,則BD2=BG2+DG2=(BO-OG)2+OD2-OG2,所以S=AB2=  BD2=7+
BD2=7+ 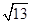 x,因為-1≤x≤1,所以S的最大值就可以求出.
x,因為-1≤x≤1,所以S的最大值就可以求出.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
 |
| AB |
 點A、點B重合).連接AC、BC,分別與⊙M相交于點D、點E,連接DE.若AB=2
點A、點B重合).連接AC、BC,分別與⊙M相交于點D、點E,連接DE.若AB=2| 3 |
| AD |
| DC |
查看答案和解析>>
科目:初中數學 來源: 題型:
 已知⊙O的半徑為1,以O為原點,建立如圖所示的直角坐標系.有一個正方形ABCD,頂點B的坐標為(-
已知⊙O的半徑為1,以O為原點,建立如圖所示的直角坐標系.有一個正方形ABCD,頂點B的坐標為(-| 13 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 |
| AOB |
 |
| BCA |
| ||
| 2 |
| ||
| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com