已知:m是非負數,拋物線y=x2-2(m+1)x-(m+3)的頂點Q在直線y=-2x-2上,且和x軸交于點A、B(點A在點B的左側).
(1)求A、B、Q三點的坐標.
(2)如果點P的坐標為(1,1).求證:PA和直線y=-2x-2垂直.
(3)點M(x,1)在拋物線上,判斷∠AMB和∠BAQ的大小關系,并說明理由.
【答案】
分析:(1)可根據公式法,表示出拋物線的頂點坐標,已知拋物線頂點在直線y=-2x-2上,可將頂點Q的坐標代入直線的解析式中,即可求得m的值,由此確定拋物線的解析式,進而得到A、B、Q三點的坐標;
(2)將A點坐標代入直線y=-2x-2中發現,A點正好在此直線的函數圖象上;可根據A、P、Q三點的坐標,分別求出AP、AQ、PQ的長,然后用勾股定理來判斷△APQ是否為直角三角形,由此可得出本題所求的結論;
(3)根據拋物線的解析式,可確定點M的坐標,進而可求得PM的長,此時發現PM=PA=PB,那么M、A、B三點共圓,在(2)中已經證得PA⊥AQ,則AQ是⊙P的切線,由弦切角定理即可得到∠AMB=∠BAQ.
解答:解:(1)設拋物線的頂點Q的坐標是(x,y),
則x=-
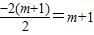
,y=
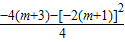
=-m
2-3m-4;
∵點Q(m+1,-m
2-3m-4)在直線y=-2x-2上,
∴-m
2-3m-4=-2(m+1)-2,
解得m
1=0,m
2=-1;
∵m是非負數,舍去m
2=-1,
∴m=0;
∵拋物線解析式為y=x
2-2x-3,令y=0,
∴得x
2-2x-3=0,
解得x
1=-1,x
2=3,
∴A(-1,0),B(3,0),Q(1,-4);
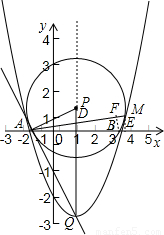
(2)如圖,∵拋物線的對稱軸是直線x=1,
∴P點在對稱軸上,
∴PQ=|1-(-4)|=5;
把A(-1,0)代入y=-2x-2,-2x(-1)-2=0成立,
∴A點在直線y=-2x-2上;
設PQ交x軸于點D,則PQ⊥AB;
在Rt△ADQ中,AQ
2=AD
2+QD
2=20,
在Rt△APD中,AP
2=AD
2+PD
2=5,
∴AQ
2+AP
2=20+5=25=PQ
2;
∴△PAQ是直角三角形,∠PAQ=90°;
∴PA⊥AQ,
∴PA和直線y=-2x-2垂直;
(3)答:∠AMB=∠BAQ;
解法一:
M(x,1)在拋物線y=x
2-2x-3上,
∴1=x
2-2x-3,
解得x=
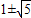
,
∴點M的坐標為(
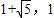
),PM=|
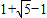
|=
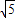
,
∴PA=PM=PB=
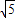
;
于是點A、M、B都在以點P為圓心,
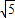
為半徑的圓上,如圖,
∵AQ⊥AP,
∴AQ是⊙P的切線,
∴∠BAQ=∠AMB;
當x=
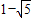
時,點M的坐標為(
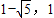
);
同理可得∠BAQ=∠AMB.(15分)
解法二;當x=1+
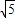
時,作ME⊥x軸于點E,如圖,則點E的坐標為(1+

,0);
于是ME=1,EA=1
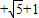
=
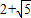
,
AM=
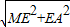
=
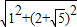
=
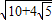
,
連接BM,作BF⊥AM于F,AB=|3-(-1)|=4,
則S
△ABM=

ME•AB=

AM•BF
∴1×4=
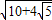
•BF
∴BF=
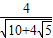
在△MBE中,∠MEB=90°,
BM=
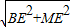
=
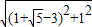
=
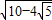
在△BFM中,∠BFM=90°,
sin∠BMF=
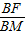
=
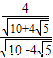
=
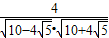
=
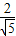
在△DAQ中,∠ADQ=90°,
∵sin∠DAQ=
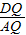
=
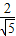
,
∴sin∠BMF=sin∠DAQ
而∠BMF、∠DAQ都是銳角,
∴∠BMF=∠DAQ,即∠AMB=∠BAQ;
當x=
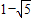
時,同解法一.
點評:此題主要考查了二次函數解析式的確定、勾股定理、直角三角形的判定和性質、切線的判定、弦切角定理等重要知識點,綜合性強,難度較大.

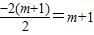 ,y=
,y=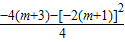 =-m2-3m-4;
=-m2-3m-4;
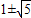 ,
,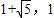 ),PM=|
),PM=|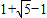 |=
|=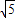 ,
,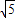 ;
;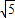 為半徑的圓上,如圖,
為半徑的圓上,如圖,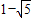 時,點M的坐標為(
時,點M的坐標為(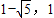 );
);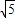 時,作ME⊥x軸于點E,如圖,則點E的坐標為(1+
時,作ME⊥x軸于點E,如圖,則點E的坐標為(1+ ,0);
,0);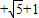 =
=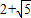 ,
,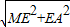 =
=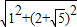 =
=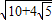 ,
, ME•AB=
ME•AB= AM•BF
AM•BF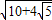 •BF
•BF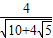
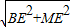 =
=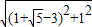 =
=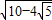
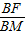 =
=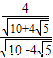 =
=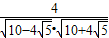 =
=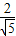
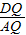 =
=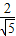 ,
,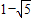 時,同解法一.
時,同解法一.
