
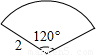
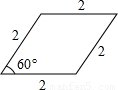
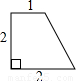
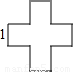
連接一個幾何圖形上任意兩點間的線段中,最長的線段稱為這個幾何圖形的直徑,根據此定義,圖(扇形、菱形、直角梯形、紅十字圖標)中“直徑”最小的是( )
|
| A. |
| B. |
| C. |
| D. |
|
考點:
菱形的性質;勾股定理;直角梯形.
分析:
先找出每個圖形的“直徑”,再根據所學的定理求出其長度,最后進行比較即可.
解答:
解: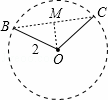
連接BC,則BC為這個幾何圖形的直徑,過O作OM⊥BC于M
∵OB=OC,
∴∠BOM=![]() ∠BOC=60°,
∠BOC=60°,
∴∠OBM=30°,
∵OB=2,OM⊥BC,
∴OM=![]() OB=1,由勾股定理得:BM=
OB=1,由勾股定理得:BM=![]() ,
,
∴由垂徑定理得:BC=2![]() ;
;
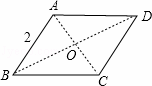
連接AC、BD,則BD為這個圖形的直徑,
∵四邊形ABCD是菱形,
∴AC⊥BD,BD平分∠ABC,
∵∠ABC=60°,
∴∠ABO=30°,
∴AO=![]() AB=1,由勾股定理得:BO=
AB=1,由勾股定理得:BO=![]() ,
,
∴BD=2BO=2![]() ;
;
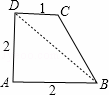
連接BD,則BD為這個圖形的直徑,
由勾股定理得:BD=![]() =2
=2![]() ;
;
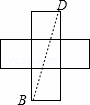
連接BD,則BD為這個圖形的直徑,
由勾股定理得:BD=![]() =
=![]() ,
,
∵2![]() >
>![]() >2
>2![]() ,
,
∴選項A、B、D錯誤,選項C正確;
故選C.
點評:
本題考查了菱形性質,勾股定理,含30度角的直角三角形性質,扇形性質等知識點的應用,主要考查學生的理解能力和推理能力.


科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源:2013年初中畢業升學考試(湖南常德卷)數學(帶解析) 題型:單選題
連接一個幾何圖形上任意兩點間的線段中,最長的線段稱為這個幾何圖形的直徑,根據此定義,圖(扇形、菱形、直角梯形、紅十字圖標)中“直徑”最小的是
A.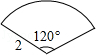 | B.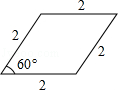 | C.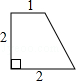 | D.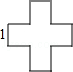 |
查看答案和解析>>
科目:初中數學 來源:2013年初中畢業升學考試(湖南常德卷)數學(解析版) 題型:選擇題
連接一個幾何圖形上任意兩點間的線段中,最長的線段稱為這個幾何圖形的直徑,根據此定義,圖(扇形、菱形、直角梯形、紅十字圖標)中“直徑”最小的是
A.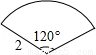 B.
B.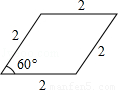 C.
C.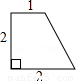 D.
D.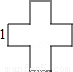
查看答案和解析>>
科目:初中數學 來源:2013年湖南省常德市中考數學試卷(解析版) 題型:選擇題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com