
【題目】在學習蘇科版九下《銳角三角函數》一章時,小明同學對一個角的倍角的三角函數值是否具有關系產生了濃厚的興趣,進行了一些研究.
(1)初步嘗試:我們知道:tan60°= ,tan30°= ,發現結論:tanA 2tan![]() ∠A(填“=”或“≠”);
∠A(填“=”或“≠”);
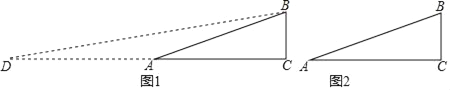
(2)實踐探究:如圖1,在Rt△ABC中,∠C=90°,AC=2,BC=1,求tan![]() ∠A的值;小明想構造包含
∠A的值;小明想構造包含![]() ∠A的直角三角形:延長CA至D,使得DA=AB,連接BD,所以得到∠D=
∠A的直角三角形:延長CA至D,使得DA=AB,連接BD,所以得到∠D=![]() ∠A,即轉化為求∠D的正切值.
∠A,即轉化為求∠D的正切值.
請按小明的思路進行余下的求解:
(3)拓展延伸:如圖2,在Rt△ABC中,∠C=90°,AC=3,tanA=![]() .
.
①tan2A= ;
②求tan3A的值.
【答案】(1)![]() ,
,![]() ,≠;(2)
,≠;(2)![]() ﹣2;(3)①
﹣2;(3)①![]() ;②
;②![]() .
.
【解析】
(1)直接利用特殊角的三角函數值得結論;
(2)根據題意,利用勾股定理求AC,得結論;
(3)①作AB的垂直平分線交AC于E,連接BE,則∠BEC=2∠A,在Rt△EBC中,利用勾股定理求出EC,求tan∠BEC得結果;
②作BM交AC于點M,使∠MBE=∠EBA,則∠BMC=3∠A.利用角平分線的性質和勾股定理求出EM的長,求tan∠BMC得結果.
(1)tan60°=![]() ,tan30°=
,tan30°=![]() ,
,
發現結論:tanA≠2tan![]() ∠A,
∠A,
故答案為:![]() ,
,![]() ,≠;
,≠;
(2)在Rt△ABC中,∠C=90°,AC=2,BC=1,
∴AB=![]() =
=![]() ,
,
如圖1,延長CA至D,使得DA=AB,
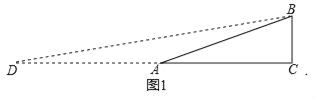
∴AD=AB=![]() ,
,
∴∠D=∠ABD,
∴∠BAC=2∠D,CD=AD+AC=2+![]() ,
,
∴tan![]() ∠A=tan∠D=
∠A=tan∠D=![]() =
=![]() ﹣2;
﹣2;
(3)①如圖2,作AB的垂直平分線交AC于E,連接BE,
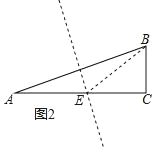
則∠BEC=2∠A,AE=BE,∠A=∠ABE
∵Rt△ABC中,∠C=90°,AC=3,tanA=![]() ,
,
∴BC=1,AB=![]() ,
,
設AE=x,則EC=3﹣x,
在Rt△EBC中,x2=(3﹣x)2+1,
解得x=![]() ,即AE=BE=
,即AE=BE=![]() ,EC=
,EC=![]() ,
,
∴tan2A=tan∠BEC=![]() =
=![]() ,
,
故答案為:![]() ;
;
②如圖3,作BM交AC于點M,使∠MBE=∠EBA,

則∠BMC=∠A+∠MBA=3∠A.
設EM=y,則MC=EC﹣EM=![]() ﹣y,
﹣y,
∵∠MBE=∠EBA,
∴![]() ,即
,即![]() ,
,
∴BM=![]() y,
y,
在Rt△MBC中,BM2=CM2+BC2
即(![]() y)2=(
y)2=(![]() ﹣y)2+1,
﹣y)2+1,
整理,得117y2+120y﹣125=0,
解得,y1=![]() ,y2=﹣
,y2=﹣![]() (不合題意,舍去)
(不合題意,舍去)
即EM=![]() ,CM=
,CM=![]() ﹣
﹣![]() =
=![]() ,
,
∴tan3A=tan∠BMC=![]() ,
,
=![]() =
=![]() .
.


科目:初中數學 來源: 題型:
【題目】請判斷下列問題中,哪些是反比例函數,并說明你的依據.
(1)三角形的底邊一定時,它的面積和這個底邊上的高;
(2)梯形的面積一定時,它的中位線與高;
(3)當矩形的周長一定時,該矩形的長與寬.
查看答案和解析>>
科目:初中數學 來源: 題型:
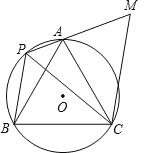
【題目】如圖,等邊△ABC 內接于⊙O,P 是![]() 上任一點(點 P 不與點 A、B 重合),連 AP、BP,過點 C 作 CM∥BP 交 PA 的延長線于點 M.
上任一點(點 P 不與點 A、B 重合),連 AP、BP,過點 C 作 CM∥BP 交 PA 的延長線于點 M.
(1)填空:∠APC= 度,∠BPC= 度;
(2)求證:△ACM≌△BCP;
(3)若 PA=1,PB=2,求梯形 PBCM 的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
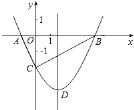
【題目】如圖,拋物線y=![]() x2+bx﹣2與x軸交于A,B兩點,與y軸交于C點,且A(﹣1,0).
x2+bx﹣2與x軸交于A,B兩點,與y軸交于C點,且A(﹣1,0).
(1)求拋物線的解析式及頂點D的坐標;
(2)判斷△ABC的形狀,證明你的結論;
(3)點M是拋物線對稱軸上的一個動點,當MC+MA的值最小時,求點M的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
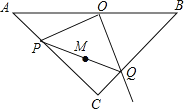
【題目】如圖,等腰Rt△ABC中,斜邊AB的長為2,O為AB的中點,P為AC邊上的動點,OQ⊥OP交BC于點Q,M為PQ的中點,當點P從點A運動到點C時,點M所經過的路線長為( )
A. ![]() B.
B. ![]() C. 1 D. 2
C. 1 D. 2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列命題:
①在函數:y=-2x-1;y=3x;y=![]() ;y=-
;y=-![]() ;y=
;y=![]() (x<0)中,y隨x增大而減小的有3個函數;
(x<0)中,y隨x增大而減小的有3個函數;
②對角線互相垂直平分且相等的四邊形是正方形;
③反比例函數圖象是兩條無限接近坐標軸的曲線,它只是中心對稱圖形;
④已知數據x1、x2、x3的方差為s2,則數據x1+2,x3+2,x3+2的方差為s3+2.
其中是真命題的個數是( )
A.1個 B.2個 C.3個 D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線y=ax2+bx+c(a≠0)的對稱軸為直線x=2,與x軸的一個交點坐標(4,0),其部分圖象如圖所示,下列結論:①拋物線過原點;②a﹣b+c<0;③4a+b+c=0;④拋物線的頂點坐標為(2,b);⑤當x<1時,y隨x增大而增大.其中結論正確的是( )
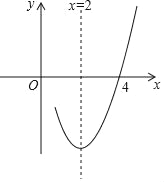
A. ①②③ B. ①④⑤ C. ①③④ D. ③④⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,梯形ABCD中,AB∥CD,∠ABC=90°,AB=8,CD=6,BC=4,AB邊上有一動點P(不與A、B重合),連結DP,作PQ⊥DP,使得PQ交射線BC于點E,設AP=x.
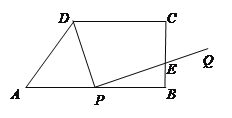
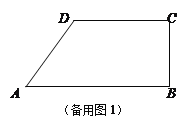

⑴當x為何值時,△APD是等腰三角形?
⑵若設BE=y,求y關于x的函數關系式;
⑶若BC的長可以變化,在現在的條件下,是否存在點P,使得PQ經過點C?若存在,求出相應的AP的長;若不存在,請說明理由,并直接寫出當BC的長在什么范圍內時,可以存在這樣的點P,使得PQ經過點C.
查看答案和解析>>
科目:初中數學 來源: 題型:
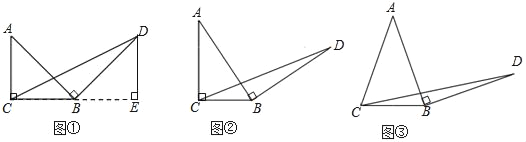
【題目】請認真閱讀下面的數學小探究系列,完成所提出的問題:
(1)探究1,如圖①,在等腰直角三角形ABC中,∠ACB=90°,BC=3,將邊AB繞點B順時針旋轉90°得到線段BD,連接CD,過點D做BC邊上的高DE,則DE與BC的數量關系是 ,△BCD的面積為 ;
(2)探究2,如圖②,在一般的Rt△ABC中,∠ACB=90°,BC=a,將邊AB繞點B順時針旋轉90°得到線段BD,連接CD,請用含a的式子表示△BCD的面積,并說明理由;
(3)探究3:如圖③,在等腰三角形ABC中,AB=AC,BC=a,將邊AB繞點B順時針旋轉90°得到線段BD,連接CD,試探究用含a的式子表示△BCD的面積,要有探究過程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com