Question

14．如圖，矩形紙片ABCD，DC=8，AD=6．
（1）如圖（1），點E在邊AD上且AE=2，以點E為頂點作正方形EFGH，頂點F，H分別在矩形ABCD的邊AB，CD上，連接CG，求∠HCG的度數；
（2）請從A、B兩題中任選一題解答，我選擇A（或B）．
A．如圖（2），甲同學把矩形紙片ABCD的四個角向內折起，恰好拼成一個無縫隙無重疊的四邊形MPNQ，判斷并說明四邊形MPNQ的形狀．
B．如圖（3），乙同學把（1）中的“正方形EFGH”改為“菱形EFGH”，其余條件不變，此時點G落在矩形ABCD的外部，已知△CGH的面積是4，求菱形EFGH的邊長及面積．

Answer 1

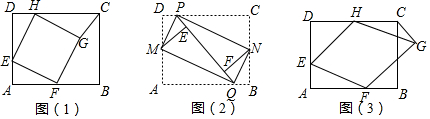
分析 （1）先根據條件判定△AFE≌△DEH≌△KHG，得出AE=DH=GK=2，DE=HK，進而得出GK=CK，即△CGK為等腰直角三角形，據此得出∠HCG的度數；
（2）①若選A題，則根據折疊的性質，求得∠PMQ=∠PME+∠QME=$\frac{1}{2}$∠DME+$\frac{1}{2}$∠AME=$\frac{1}{2}$∠AMD=90°，同理可得，∠MQN=90°，∠PNQ=90°，進而得出四邊形MPNQ的形狀是矩形；
②若選B題，則需要連接HF，過G作GP⊥CD的延長線于P，再根據矩形和菱形的性質，判定△AEF≌△PGH（AAS），得出PG=AE=2，再根據△CGH的面積是4，求得CH的長，進而在Rt△DEH中，根據勾股定理得出EH=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$，即菱形EFGH的邊長為4$\sqrt{2}$，最后根據菱形EFGH的面積=2×△EFH的面積=2×（四邊形ADHF的面積-△DEH的面積-△AEF的面積），進行計算求解即可．

解答 解：（1）過點G作GK⊥CD于點K，
∵四邊形ABCD為矩形，DC=8，AD=6，
∴∠A=∠D=∠HKG=90°，
∵四邊形EFGH為正方形，
∴∠FEH=∠EHG=90°，EF=EH=HG，
∴∠AFE=∠DEH=∠KHG，
∴△AFE≌△DEH≌△KHG，
∴AE=DH=GK=2，DE=HK，
∵DC=8，AD=6，
∴CK=DC-DH=8-6=2，
∴GK=CK，
∴∠KCG=∠CGK=45°，
即∠HCG的度數是45°；

（2）選A題，四邊形MPNQ的形狀是矩形．
證明：如圖2，∵四邊形ABCD為矩形，
∴∠A=∠D=90°，
∵DM與EM重合，AM與EM重合，
∴PM平分∠DME，QM平分∠AME，
∴∠PMQ=∠PME+∠QME=$\frac{1}{2}$∠DME+$\frac{1}{2}$∠AME=$\frac{1}{2}$∠AMD=90°，
同理可得，∠MQN=90°，∠PNQ=90°，
∴四邊形MPNQ的形狀是矩形．

選B題，
如圖3，連接HF，過G作GP⊥CD的延長線于P，
∵四邊形ABCD為矩形，
∴AB∥CD，∠A=∠D=90°，
∴∠AFH=∠PHF，
∵四邊形EFGH為菱形，
∴EF∥HG，EF=HG，
∴∠1=∠2，
∴∠AFE=∠PHG，
又∵GP⊥DP，
∴∠P=∠A=90°，
在△AEF和△PGH中，
$\left\{\begin{array}{l}{∠A=∠P}\\{∠AFE=∠PHG}\\{EF=HG}\end{array}\right.$，
∴△AEF≌△PGH（AAS），
∴PG=AE=2，
∵△CGH的面積是4，
∴$\frac{1}{2}$×HC×PG=4，
∴HC=4，
∵CD=8，AD=6，AE=2，
∴DH=8-4=4，DE=6-2=4，
∴Rt△DEH中，EH=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$，
∴EF=4$\sqrt{2}$，即菱形EFGH的邊長為4$\sqrt{2}$，
∴Rt△AEF中，AF=$\sqrt{（4\sqrt{2}）^{2}-{2}^{2}}$=2$\sqrt{7}$，
∴菱形EFGH的面積=2×△EFH的面積
=2×（四邊形ADHF的面積-△DEH的面積-△AEF的面積）
=2×[$\frac{1}{2}$（DH+AF）×AD-$\frac{1}{2}$×DH×ED-$\frac{1}{2}$×AE×AF]
=2×[$\frac{1}{2}$（4+2$\sqrt{7}$）×6-$\frac{1}{2}$×4×4-$\frac{1}{2}$×2×2$\sqrt{7}$]
=（4+2$\sqrt{7}$）×6-4×4-2×2$\sqrt{7}$
=8+8$\sqrt{7}$．
∴菱形EFGH的邊長及面積分別為4$\sqrt{2}$和8+8$\sqrt{7}$．

點評 本題屬于四邊形綜合題，主要考查了矩形、菱形和正方形的性質，勾股定理，折疊的性質以及全等三角形的判定與性質的綜合應用，解決問題的關鍵是掌握幾種特殊四邊形的性質，通過作輔助線構造等腰直角三角形和全等三角形．解題時注意，運用割補法求菱形的面積比較合適．