某商場購進一批單價為16元的商品,經市場調查發現若按20元/件銷售,每月能售出360件,若按25元/件銷售,何月能售出210件,設每月銷售量y(件)是售價x(元/件)的一次函數.
(1)求y與x之間的函數關系式;
(2)銷售價定為多少時,才能使月利潤最大,月最大利潤是多少?
【答案】
分析:(1)設出一次函數解析式y=kx+b,用待定系數法求解即可.
(2)按照等量關系“每月獲得的利潤=(銷售價格-進價)×銷售件數”列出二次函數,并求得最值.
解答:解:(1)依題意設y=kx+b,
則有
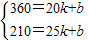
解得:
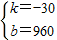
.
所以y=-30x+960(16≤x≤32);
(2)每月獲得利潤:
P=(-30x+960)(x-16)
=30(-x+32)(x-16)
=30(-x
2+48x-512)
=-30(x-24)
2+1920.
所以當x=24時,P有最大值,最大值為1920.
答:當價格為24元時,才能使每月獲得最大利潤,最大利潤為1920元.
點評:本題考查了二次函數在實際生活中的應用,重點是掌握求最值的問題.注意:數學應用題來源于實踐,用于實踐,在當今社會市場經濟的環境下,應掌握一些有關商品價格和利潤的知識,總利潤等于總收入減去總成本,然后再利用二次函數求最值.

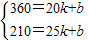
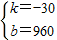 .
.
