
【題目】根據如圖所示的數軸,解答下面問題.

(1)分別寫出![]() 、
、![]() 兩點所表示的有理數;
兩點所表示的有理數;
(2)請問![]() 、
、![]() 兩點之間的距離是多少?
兩點之間的距離是多少?
(3)在數軸上畫出與![]() 點距離為2的點(用不同于
點距離為2的點(用不同于![]() 、
、![]() 的其它字母表).
的其它字母表).
【答案】(1)點![]() 表示1;點
表示1;點![]() 表示-2.5;(2)距離是3.5;(3)兩點C、D分別是-1,3,圖詳見解析.
表示-2.5;(2)距離是3.5;(3)兩點C、D分別是-1,3,圖詳見解析.
【解析】
(1)觀察數軸,即可找出A、B兩點表示的數;
(2)根據兩點的距離公式,即可求出A、B兩點之間的距離;
(3)設與A點距離為2的點表示的數為x,根據兩點間的距離公式即可得出關于x的含絕對值符號的一元一次方程,解之即可得出x的值,將其標記在數軸上即可.
解:(1)根據數軸可知點![]() 表示1;點
表示1;點![]() 表示-2.5;
表示-2.5;
(2)依題意得:AB之間的距離為:![]() =1+2.5=3.5;
=1+2.5=3.5;
(3)設與A點距離為2的點表示的數為x,
根據題意得:|x-1|=2,
解得:x=-1或x=3.
將其標記在數軸上,點C、D即為所求.



科目:初中數學 來源: 題型:
【題目】主題班會課上,王老師出示了如圖所示的一幅漫畫,經過同學們的一番熱議,達成以下四個觀點:
A.放下自我,彼此尊重; B.放下利益,彼此平衡;
C.放下性格,彼此成就; D.合理競爭,合作雙贏.
要求每人選取其中一個觀點寫出自己的感悟.根據同學們的選擇情況,小明繪制了下面兩幅不完整的圖表,請根據圖表中提供的信息,解答下列問題:

(1)參加本次討論的學生共有 人;
(2)表中![]() ,
,![]() ;
;
(3)將條形統計圖補充完整;
(4)現準備從![]() 四個觀點中任選兩個作為演講主題,請用列表或畫樹狀圖的方法求選中觀點
四個觀點中任選兩個作為演講主題,請用列表或畫樹狀圖的方法求選中觀點![]() (合理競爭,合作雙贏)的概率.
(合理競爭,合作雙贏)的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某農科所對甲、乙兩種小麥各選用10塊面積相同的試驗田進行種植試驗,它們的平均畝產量分別是![]() =610千克,
=610千克, ![]() =609千克,畝產量的方差分別是
=609千克,畝產量的方差分別是![]() =29.6,
=29.6, ![]() =2.則關于兩種小麥推廣種植的合理決策是( )
=2.則關于兩種小麥推廣種植的合理決策是( )
A. 甲的平均畝產量較高,應推廣甲
B. 甲、乙的平均畝產量相差不多,均可推廣
C. 甲的平均畝產量較高,且畝產量比較穩定,應推廣甲
D. 甲、乙的平均畝產量相差不多,但乙的畝產量比較穩定,應推廣乙
查看答案和解析>>
科目:初中數學 來源: 題型:
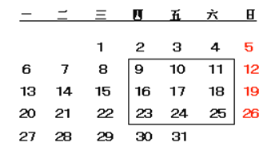
【題目】如圖:是某月份的月歷表,請你認真觀察月歷表,回答以下問題:
(1)如果圈出同一行的三個數,用a表示中間的數,則第一個數,第三個數怎樣表示?
(2)如果圈出同一列的三個數,用a表示中間的數,則第一個數,第三個數怎樣表示?
(3)如果圈出如圖所示的任意9個數,這9個數的和可能是207嗎?如果可能,請求出這9個數;如果不可能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學生的學業負擔過重會嚴重影響學生對待學習的態度.為此我市教育部門對部分學校的八年級學生對待學習的態度進行了一次抽樣調查(把學習態度分為三個層級,A級:對學習很感興趣;B級:對學習較感興趣;C級:對學習不感興趣),并將調查結果繪制成圖①和圖②的統計圖(不完整).請根據圖中提供的信息,解答下列問題:
(1)此次抽樣調查中,共調查了 名學生;
(2)將圖①補充完整;
(3)求出圖②中C級所占的圓心角的度數;
(4)根據抽樣調查結果,請你估計我市近8000名八年級學生中大約有多少名學生學習態度達標(達標包括A級和B級)?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,![]() 中,
中,![]() 是
是![]() 邊上一點,
邊上一點,![]() 是
是![]() 的中點,過點
的中點,過點![]() 作
作![]() 的平行線交
的平行線交![]() 的延長線于
的延長線于![]() ,且
,且![]() ,連接
,連接![]() .
.
(1)求證:![]() 是
是![]() 的中點;
的中點;
(2)若![]() ,試判斷四邊形
,試判斷四邊形![]() 的形狀,并證明你的結論.
的形狀,并證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
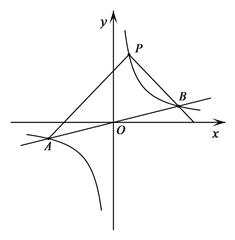
【題目】如圖,反比例函數y=![]() 的圖象與一次函數y=
的圖象與一次函數y=![]() x的圖象交于點A、B,點B的橫坐標是4.點P是第一象限內反比例函數圖象上的動點,且在直線AB的上方.
x的圖象交于點A、B,點B的橫坐標是4.點P是第一象限內反比例函數圖象上的動點,且在直線AB的上方.
(1)若點P的坐標是(1,4),直接寫出k的值和△PAB的面積;
(2)設直線PA、PB與x軸分別交于點M、N,求證:△PMN是等腰三角形;
(3)設點Q是反比例函數圖象上位于P、B之間的動點(與點P、B不重合),連接AQ、BQ,比較∠PAQ與∠PBQ的大小,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
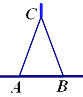
【題目】小知識:如圖,我們稱兩臂長度相等(即![]() )的圓規為等臂圓規. 當等臂圓規的兩腳擺放在一條直線上時,若張角
)的圓規為等臂圓規. 當等臂圓規的兩腳擺放在一條直線上時,若張角![]() ,則底角
,則底角![]() .
.
請運用上述知識解決問題:
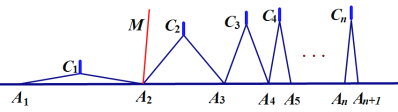
如圖,![]() 個相同規格的等臂圓規的兩腳依次擺放在同一條直線上,其張角度數變化如下:
個相同規格的等臂圓規的兩腳依次擺放在同一條直線上,其張角度數變化如下:
![]() ,
,![]() ,
, ![]() ,
,![]() ,…
,…
(1)、①由題意可得![]() = ;
= ;
②若![]() 平分
平分![]() ,則
,則![]() = ;
= ;
(2)、![]() = (用含
= (用含![]() 的代數式表示);
的代數式表示);
(3)、當![]() 時,設
時,設![]() 的度數為
的度數為![]() ,
,![]() 的角平分線
的角平分線![]() 與
與![]() 構成的角的度數為
構成的角的度數為![]() ,那么
,那么![]() 與
與![]() 之間的等量關系是 ,請說明理由. (提示:可以借助下面的局部示意圖)
之間的等量關系是 ,請說明理由. (提示:可以借助下面的局部示意圖)
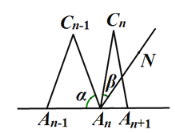
查看答案和解析>>
科目:初中數學 來源: 題型:
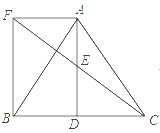
【題目】如圖,四邊形ABCD為平行四邊形,∠BAD的角平分線AE交CD于點F,交BC的延長線于點E.
(1)求證:BE=CD;
(2)連接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四邊形ABCD的面積.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com