
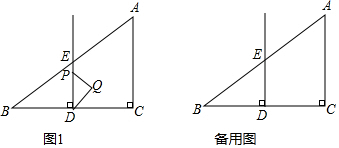
分析 (1)分兩種情況進行討論:點P在線段DE上,點P在DE的延長線上,根據線段的和差關系進行計算;
(2)當點Q落在邊AC上時,過點Q作QF⊥DP于F,根據四邊形CDFQ是矩形,△DPQ是等腰直角三角形,求得DP=2FQ=8,即可得到t的值;
(3)分兩種情況進行討論:①當點P在線段DE上時,△PDQ和△ABC重疊部分為△DPQ,②當點P在線段DE的延長線上時,△PDQ和△ABC重疊部分為四邊形EDQG,分別求得S與t之間的函數關系式.
解答 解:(1)由題可得,DP=t,DE=$\frac{1}{2}$AC=3,
當點P在線段DE上時,EP=DE-DP=3-t;
當點P在DE的延長線上時,EP=DP-DE=t-3;
(2)如圖所示,當點Q落在邊AC上時,過點Q作QF⊥DP于F,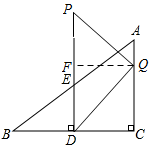
∵∠C=∠CDF=∠DFQ=90°,
∴四邊形CDFQ是矩形,
∴FQ=CD=$\frac{1}{2}$BC=4,
∵△DPQ是等腰直角三角形,
∴DP=2FQ=8,
∴t=$\frac{8}{1}$=8(s);
(3)①當點P在線段DE上時,△PDQ和△ABC重疊部分為△DPQ,且DP=t,DP邊上的高為$\frac{1}{2}$t,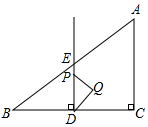
∵點P從點D運動到點E處時,時間為3s,
∴當0<t≤3時,S=$\frac{1}{2}$×t×$\frac{1}{2}$t=$\frac{1}{4}{t}^{2}$,
②當點P在線段DE的延長線上時,△PDQ和△ABC重疊部分為四邊形EDQG,
如圖所示,過G作GF⊥PE于F,則△GFE∽△BCA,且PF=GF,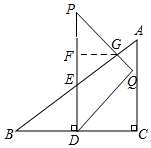
∵AC=6,BC=8,
∴EF:FG=3:4,EF:FP=3:4,
∵PE=t-3,
∴FG=$\frac{4}{7}$(t-3),
∴△PEG的面積=$\frac{1}{2}$×PE×FG=$\frac{1}{2}$×$\frac{4}{7}$(t-3)2,
由(2)可知,點Q落在邊AC上時,t的值為8s,
∴當3≤t≤8時,S=$\frac{1}{4}$t2-$\frac{1}{2}$×$\frac{4}{7}$(t-3)2=-$\frac{1}{28}$t2+$\frac{12}{7}$t-$\frac{18}{7}$.
綜上所述,S與t之間的函數關系式為:S=$\left\{\begin{array}{l}{\frac{1}{4}{t}^{2}(0<t≤3)}\\{-\frac{1}{28}{t}^{2}+\frac{12}{7}t-\frac{18}{7}(3≤t≤8)}\end{array}\right.$.
點評 本題屬于三角形綜合題,主要考查了等腰直角三角形的性質,相似三角形的判定與性質以及三角形面積的計算的綜合應用,解決問題的關鍵是作輔助線構造直角三角形,解題時注意分類討論思想的運用.


 作業輔導系列答案
作業輔導系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 3 | B. | -3 | C. | -$\frac{5}{3}$ | D. | 0 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 由7x=4x-3移項得7x-4x=3 | |
| B. | 由$\frac{2x-1}{3}$=1+$\frac{x-3}{2}$去分母得2(2x-1)=1+3(x-3) | |
| C. | 由2(2x-1)-3(x-3)=1去括號得4x-2-3x-9=1 | |
| D. | 由2(x+1)=x+7 移項、合并同類項得 x=5 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | |-33|<-32<(-3)2 | B. | |-33|<(-3)2<-32 | C. | -32<|-33|<(-3)2 | D. | -32<(-3)2<|-33| |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com