【題目】如圖，在過直線AB外一點P作直線AB的平行線時，可以按如下步驟進行：①在直線AB上任取兩點C，D；②分別以點P，D為圓心，CD與PC為半徑畫弧，兩弧交于點E；③作直線PE，則PE∥AB．在上面作圖過程中，PE∥AB的依據是________．
舉一反三期末百分沖刺卷系列答案科目：初中數學 來源： 題型：
【題目】2018年5月5日，中國郵政發行《馬克思誕辰200周年》紀念郵票1套2枚（如圖），這套郵票正面圖案為：馬克思像、馬克思與恩格斯像，背面完全相同.發行當日，小宇購買了此款紀念郵票2套，他將2套郵票沿中間虛線撕開（使4枚形狀、大小完全相同）后將4枚紀念郵票背面朝上放在桌面上，并隨機從中抽出2張，則抽出的2張郵票恰好都是“馬克思像”的概率為（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，拋物線
的圖像過點
，頂點為
求
的值．
點以點
為旋轉中心，順時針旋轉
得到點
，判斷點是否落在拋物線上．
第一象限內拋物線上有一點
與
相交于點
，當
時，求點
坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】拋物線y=﹣x2+bx+c經過點A、B、C，已知A（﹣1，0），C（0，3）．
（1）求拋物線的解析式；
（2）如圖1，P為線段BC上一點，過點P作y軸平行線，交拋物線于點D，當△BDC的面積最大時，求點P的坐標；
（3）如圖2，拋物線頂點為E，EF⊥x軸于F點，M（m，0）是x軸上一動點，N是線段EF上一點，若∠MNC=90°，請指出實數m的變化范圍，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】丁老師為了解所任教的兩個班的學生數學學習情況，對數學進行了一次測試，獲得了兩個班的成績（百分制），并對數據（成績）進行整理、描述和分析，下面給出了部分信息．①A、B兩班學生（兩個班的人數相同）數學成績不完整的頻數分布直方圖如下（數據分成 5 組：x＜60，60≤x＜70，70≤x＜80，80≤x＜90，90≤x≤100）：
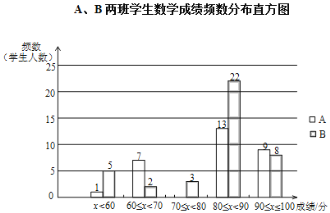
②A、B兩班學生測試成績在80≤x＜90這一組的數據如下：
A 班：80 80 82 83 85 85 86 87 87 87 88 89 89
B 班：80 80 81 81 82 82 83 84 84 85 85 86 86 86 87 87 87 87 87 88 88 89
③A、B兩班學生測試成績的平均數、中位數、方差如下：
平均數 | 中位數 | 方差 | |
A班 | 80.6 | m | 96.9 |
B班 | 80.8 | n | 153.3 |
根據以上信息，請寫出表中 m、n的值____________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀下列材料，解決所提的問題：
勾股定理a+b=c本身就是一個關于a，b，c的方程，我們知道這個方程有無數組解，滿足該方程的正整數解（a，b，c）通常叫做勾股數組．關于勾股數組的研究我國歷史上有非常輝煌的成就，根據我國古代數學書《周髀算經》記載，在約公元前1100年，人們就已經知道“勾廣三、股修四、徑隅五”（古人把較短的直角邊稱為勾，較長的直角邊稱為股，而斜邊則為弦），即知道了勾股數組（3，4，5）．類似地，還可以得到下列勾股數組：（3，4，5），（5，12，13），（7，24，25），（9，40，41），…等等，這些數組也叫做畢達哥拉斯勾股數組．
上述勾股數組的規律，可以用下面表格直觀表示：
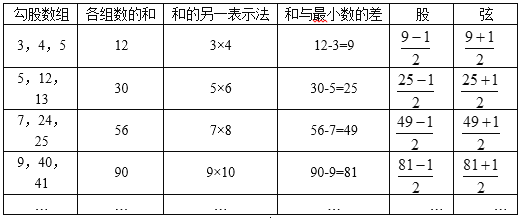
觀察分析上述勾股數組，可以看出它們具有如下特點：
特點1：最小的勾股數的平方等于另兩個勾股數的和；
特點2：____________________________________．
…
學習任務：
（1）請你再寫出上述勾股數組的一個特點：________________；
（2）如果n表示比1大的奇數，則上述勾股數組可以表示為（n，______，______）
（3）請你證明（2）的結論．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，方格紙中的每個小方格都是邊長為1個單位的正方形，在建立平面直角坐標系后，△ABC的頂點均在格點上，點B的坐標為（1,0）
（1）畫出△ABC關于x軸對稱的△A1B1C1，
（2）畫出將△ABC繞原點O按逆時針旋轉90°所得的△A2B2C2，
（3）△A1B1C1與△A2B2C2成軸對稱圖形嗎？若成軸對稱圖形，畫出所有的對稱軸并寫出對稱軸；
（4）△A1B1C1與△A2B2C2成中心對稱圖形嗎？若成中心對稱圖形，寫出所有的對稱中心的坐標.
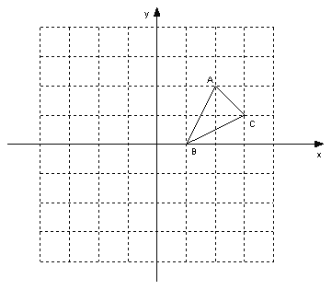
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，一艘輪船以每小時40海里的速度在海面上航行，當該輪船行駛到B處時，發現燈塔C在它的東北方向，輪船繼續向北航行，30分鐘后到達A處，此時發現燈塔C在它的北偏東75°方向上，求此時輪船與燈塔C的距離．（結果保留根號）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，拋物線的頂點A的坐標為（1，4），拋物線與x軸相交于B、C兩點，與y軸交于點E（0，3）．
（1）求拋物線的表達式；
（2）已知點F（0，﹣3），在拋物線的對稱軸上是否存在一點G，使得EG+FG最小，如果存在，求出點G的坐標；如果不存在，請說明理由．
（3）如圖2，連接AB，若點P是線段OE上的一動點，過點P作線段AB的垂線，分別與線段AB、拋物線相交于點M、N（點M、N都在拋物線對稱軸的右側），當MN最大時，求△PON的面積．
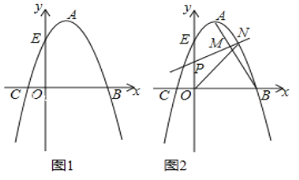
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
