
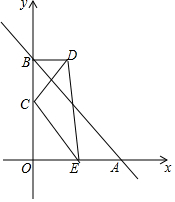 如圖,在平面直角坐標系中,直線AB與x軸交于點A(4,0),與y軸交于點B(0,4),點E(2,0)在OA上,點C的坐標為(0,m)(m≠4),點C關于AB的對稱點是點D,連結BD,CD,CE,DE
如圖,在平面直角坐標系中,直線AB與x軸交于點A(4,0),與y軸交于點B(0,4),點E(2,0)在OA上,點C的坐標為(0,m)(m≠4),點C關于AB的對稱點是點D,連結BD,CD,CE,DE分析 (1)由A(4,0),B(0,4),得出OB=OA=4,∠OBA=45°,因為點D與點C關于直線AB對稱,即可證得結論;
(2)分兩種情況分別討論,根據等腰直角三角形的性質求得m的值,進而就可得出結論.
解答 (1)證明:如圖,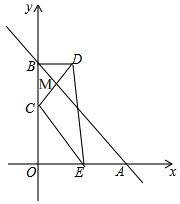
∵A(4,0)B(0,4),
∴OB=OA=4,∠OBA=45°,
∵點D與點C關于直線AB對稱,令交點為M,
∴DM=CM,CD⊥AB于M,
∴∠BCM=45°,BC=BD,∠BDC=45°
∴△BCD為等腰直角三角形;
(2)解:∵E(2,0),
∴OE=2,
(Ⅰ)當∠DCE=90°時,如圖1,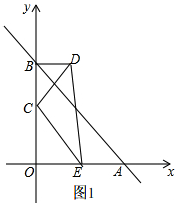
∵∠BCD=45°,
∴∠OCE=45°,△OCE為等腰直角三角形,
∴∠CEO=45°
∴OC=OE=2,
∴$\frac{OC}{OE}$=1;
(Ⅱ)當∠CDE=90°時,如圖2,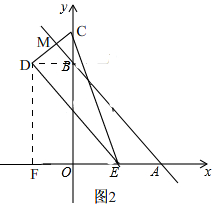
作DF⊥x軸于點F,
∵∠CMB=∠CDE=90°,
∴AB∥DE
∴∠DEF=∠BAO=45°,△DFE為等腰直角三角形
∴EF=DF=OB=4,
∴OF=DB=CB=2,
∴m=OC=OB+BC=6,
∵OE=2
∴$\frac{OC}{OE}$=$\frac{6}{2}$=3;
∴$\frac{OC}{OE}$的值為1或3.
點評 此題是一次函數綜合題,主要考查了等腰直角三角形的判定和性質,直角三角形的性質,對稱的性質,解本題的關鍵是求出m的值,是一道中等難度的題目.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:選擇題
| A. | y=(x-1)2+3 | B. | y=(x+1)2+3 | C. | y=x2+2 | D. | y=x2+4 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
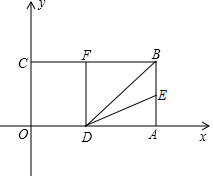 如圖,以長方形OABC的頂點O為原點,OA所在直線為x軸,OC所在直線為y軸,建立平面直角坐標系.已知OA=3,OC=2,點E是AB的中點,在OA上取一點D,連結BD,點A關于BD的對稱點恰好落在線段BC邊上的點F處.
如圖,以長方形OABC的頂點O為原點,OA所在直線為x軸,OC所在直線為y軸,建立平面直角坐標系.已知OA=3,OC=2,點E是AB的中點,在OA上取一點D,連結BD,點A關于BD的對稱點恰好落在線段BC邊上的點F處.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
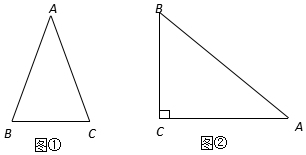 通過學習三角函數,我們知道在直角三角形中,一個銳角的大小與兩條邊長的比值相互唯一確定,因此邊長與角的大小之間可以相互轉化.類似的,可以在等腰三角形中建立邊角之間的聯系.我們定義:等腰三角形中底邊與腰的比叫做頂角的正對(sad).如圖①在△ABC中,AB=AC,頂角A的正對記作sadA,這時sadA=$\frac{底邊}{腰}=\frac{BC}{AB}$.容易知道一個角的大小與這個角的正對值也是相互唯一確定的.根據上述角的正對定義,解下列問題:
通過學習三角函數,我們知道在直角三角形中,一個銳角的大小與兩條邊長的比值相互唯一確定,因此邊長與角的大小之間可以相互轉化.類似的,可以在等腰三角形中建立邊角之間的聯系.我們定義:等腰三角形中底邊與腰的比叫做頂角的正對(sad).如圖①在△ABC中,AB=AC,頂角A的正對記作sadA,這時sadA=$\frac{底邊}{腰}=\frac{BC}{AB}$.容易知道一個角的大小與這個角的正對值也是相互唯一確定的.根據上述角的正對定義,解下列問題:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
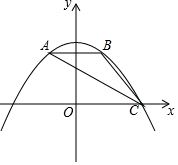 如圖,拋物線y=ax2+$\frac{9}{4}$經過△ABC的三個頂點,點A坐標為(-1,2),點B是點A關于y軸的對稱點,點C在x軸的正半軸上.
如圖,拋物線y=ax2+$\frac{9}{4}$經過△ABC的三個頂點,點A坐標為(-1,2),點B是點A關于y軸的對稱點,點C在x軸的正半軸上.查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com