Question

5．我們將能完全覆蓋某平面圖形的最小圓稱為該平面圖形的最小覆蓋圓．例如線段AB的最小覆蓋圓就是以線段AB為直徑的圓．

（1）請分別作出圖①中兩個三角形的最小覆蓋圓（要求用尺規作圖，保留作圖痕跡，不寫作法）；
（2）三角形的最小覆蓋圓有何規律？請直接寫出你所得到的結論（不要求證明）；
（3）某城市有四個小區E，F，G，H（其位置如圖②所示），現擬建一個手機信號基站，為了使這四個小區居民的手機都能有信號，且使基站所需發射功率最小（距離越小，所需功率越小），此基站應建在何處？請寫出你的結論并說明研究思路．

Answer 1

分析 （1）本題關鍵要確定最小覆蓋圓的半徑，然后才能作答；
（2）中轉站應建在△EFH的外接圓圓心處（線段EF的垂直平分線與線段EH的垂直平分線的交點處）；
（3）根據△EFH是銳角三角形，可知其最小覆蓋圓為△EFH的外接圓，所以中轉站建在△EFH的外接圓圓心處，能夠符合題中要求．

解答 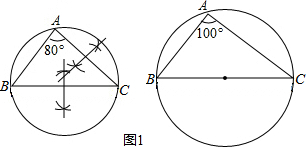解：（1）如圖所示：

（2）若三角形為銳角三角形，則其最小覆蓋圓為其外接圓；
若三角形為直角或鈍角三角形，則其最小覆蓋圓是以三角形最長邊（直角或鈍角所對的邊）為直徑的圓．

（3）此中轉站應建在△EFH的外接圓圓心處（線段EF的垂直平分線與線段EH的垂直平分線的交點處）．
理由如下
∠HEF=∠HEG+∠GEF=48°+33.88°=81.88°，
∠EHF=50°，∠EFB=48.12°，
∴△EFH是銳角三角形，所以其最小覆蓋圓為△EFH的外接圓，
設此外接圓為⊙O，直線EG與⊙O交于點E，M，則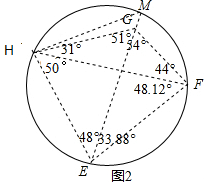
∠
故點G在⊙O內，從而⊙O也是四邊形EFGH的最小覆蓋圓．
所以中轉站建在△EFH的外接圓圓心處，能夠符合題中要求．

點評 本題考查了三角形外接圓的性質，關鍵要懂得何為最小覆蓋圓．知道若三角形為銳角三角形，則其最小覆蓋圓為其外接圓；若三角形為直角或鈍角三角形，則其最小覆蓋圓是以三角形最長邊（直角或鈍角所對的邊）為直徑的圓是解題的關鍵．