
科目:初中數學 來源:2012年初中畢業升學考試(江蘇鹽城卷)數學(帶解析) 題型:解答題
知識遷移
當 且
且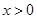 時,因為
時,因為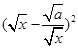 ≥
≥ ,所以
,所以 ≥
≥ ,從而
,從而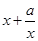 ≥
≥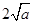 (當
(當 時取等號).
時取等號).
記函數 ,由上述結論可知:當
,由上述結論可知:當 時,該函數有最小值為
時,該函數有最小值為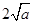
直接應用
已知函數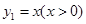 與函數
與函數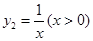 , 則當
, 則當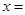 ____時,
____時,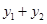 取得最小值為___.
取得最小值為___.
變形應用
已知函數 與函數
與函數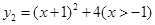 ,求
,求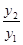 的最小值,并指出取得
的最小值,并指出取得
該最小值時相應的 的值.
的值.
實際應用
已知某汽車的一次運輸成本包含以下三個部分:一是固定費用,共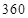 元;二是燃油費,每千
元;二是燃油費,每千
米為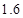 元;三是折舊費,它與路程的平方成正比,比例系數為
元;三是折舊費,它與路程的平方成正比,比例系數為 .設該汽車一次運輸的路
.設該汽車一次運輸的路
程為 千米,求當
千米,求當 為多少時,該汽車平均每千米的運輸成本最低?最低是多少元?
為多少時,該汽車平均每千米的運輸成本最低?最低是多少元?
查看答案和解析>>
科目:初中數學 來源:2011-2012學年江蘇鹽城第一初級中學九年級下學期期中考試數學卷(帶解析) 題型:解答題
(本題滿分12分)
問題情境
已知矩形的面積為a(a為常數,a>0),當該矩形的長為多少時,它的周長最小?最小值是多少?
數學模型
設該矩形的長為x,周長為y,則y與x的函數關系式為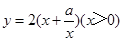 .
.
探索研究
⑴我們可以借鑒以前研究函數的經驗,先探索函數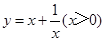 的圖象性質.
的圖象性質.
① 填寫下表,畫出函數的圖象:
| x | … | 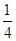 | 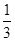 | 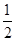 | 1 | 2 | 3 | 4 | … |
| y | … | | | | | | | | … |
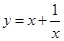 (x>0)的最小值.
(x>0)的最小值.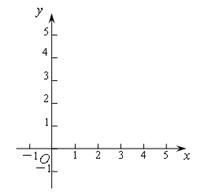
查看答案和解析>>
科目:初中數學 來源:2012年初中畢業升學考試(江蘇鹽城卷)數學(解析版) 題型:解答題
知識遷移
當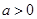 且
且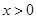 時,因為
時,因為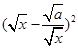 ≥
≥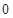 ,所以
,所以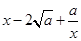 ≥
≥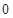 ,從而
,從而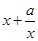 ≥
≥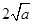 (當
(當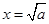 時取等號).
時取等號).
記函數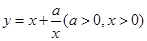 ,由上述結論可知:當
,由上述結論可知:當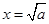 時,該函數有最小值為
時,該函數有最小值為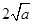
直接應用
已知函數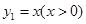 與函數
與函數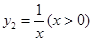 , 則當
, 則當 ____時,
____時,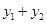 取得最小值為___.
取得最小值為___.
變形應用
已知函數 與函數
與函數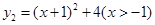 ,求
,求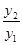 的最小值,并指出取得
的最小值,并指出取得
該最小值時相應的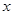 的值.
的值.
實際應用
已知某汽車的一次運輸成本包含以下三個部分:一是固定費用,共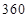 元;二是燃油費,每千
元;二是燃油費,每千
米為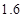 元;三是折舊費,它與路程的平方成正比,比例系數為
元;三是折舊費,它與路程的平方成正比,比例系數為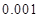 .設該汽車一次運輸的路
.設該汽車一次運輸的路
程為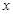 千米,求當
千米,求當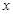 為多少時,該汽車平均每千米的運輸成本最低?最低是多少元?
為多少時,該汽車平均每千米的運輸成本最低?最低是多少元?
查看答案和解析>>
科目:初中數學 來源:江蘇中考真題 題型:解答題
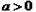 且
且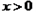 時,因為
時,因為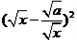 ≥
≥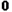 ,所以
,所以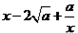 ≥
≥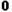 ,從而
,從而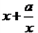 ≥
≥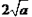 (當
(當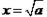 時取等號).
時取等號).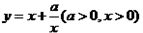 ,由上述結論可知:當
,由上述結論可知:當 時,該函數有最小值為
時,該函數有最小值為
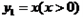 與函數
與函數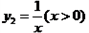 , 則當
, 則當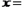 ( )時,
( )時,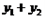 取得最小值為( )
取得最小值為( )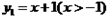 與函數
與函數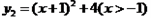 ,求
,求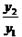 的最小值,并指出取得該最小值時相應的
的最小值,并指出取得該最小值時相應的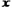 的值
的值 元;二是燃油費,每千米為
元;二是燃油費,每千米為 元;三是折舊費,它與路程的平方成正比,比例系數為
元;三是折舊費,它與路程的平方成正比,比例系數為 .設該汽車一次運輸的路程為
.設該汽車一次運輸的路程為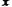 千米,求當
千米,求當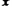 為多少時,該汽車平均每千米的運輸成本最低?最低是多少元?
為多少時,該汽車平均每千米的運輸成本最低?最低是多少元?查看答案和解析>>
科目:初中數學 來源: 題型:
知識遷移
當![]() 且
且![]() 時,因為
時,因為![]() ≥
≥![]() ,所以
,所以![]() ≥
≥![]() ,
,
從而![]() ≥
≥![]() (當
(當![]() 時取等號).
時取等號).
記函數![]() ,由上述結論可知:當
,由上述結論可知:當![]() 時,該函數有最小值為
時,該函數有最小值為![]() .
.
直接應用
已知函數![]() 與函數
與函數![]() , 則當
, 則當![]() _________時,
_________時,![]() 取得最小值為_________.
取得最小值為_________.
變形應用
已知函數![]() 與函數
與函數![]() ,求
,求![]() 的最小值,并指出取得該最小值時相應的
的最小值,并指出取得該最小值時相應的![]() 的值.
的值.
實際應用
已知某汽車的一次運輸成本包含以下三個部分:一是固定費用,共![]() 元;二是燃油費,每千米為
元;二是燃油費,每千米為![]() 元;三是折舊費,它與路程的平方成正比,比例系數為
元;三是折舊費,它與路程的平方成正比,比例系數為![]() .設該汽車一次運輸的路程為
.設該汽車一次運輸的路程為![]() 千米,求當
千米,求當![]() 為多少時,該汽車平均每千米的運輸成本最低?最低是多少元?
為多少時,該汽車平均每千米的運輸成本最低?最低是多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com