
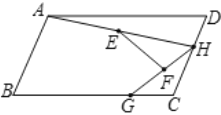
【題目】如圖,在平行四邊形![]() 中,
中,![]() ,
,![]() ,點
,點![]() 、
、![]() 分別是邊
分別是邊![]() 、
、![]() 上的動點.連接
上的動點.連接![]() 、
、![]() ,點
,點![]() 為
為![]() 的中點,點
的中點,點![]() 為
為![]() 的中點,連接
的中點,連接![]() .則
.則![]() 的最大值與最小值的差為( )
的最大值與最小值的差為( )
A.2B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
如圖,取AD的中點M,連接CM、AG、AC,作AN⊥BC于N.首先證明∠ACD=90°,求出AC,AN,利用三角形中位線定理,可知EF=![]() AG,求出AG的最大值以及最小值即可解決問題.
AG,求出AG的最大值以及最小值即可解決問題.
解:如圖,取AD的中點M,連接CM、AG、AC,作AN⊥BC于N.
∵四邊形ABCD是平行四邊形,∠BCD=120°,![]()
∴∠D=180°∠BCD=60°,AB=CD=4,
∵AM=DM=DC=4,
∴△CDM是等邊三角形,
∴∠DMC=∠MCD=60°,AM=MC,
∴∠MAC=∠MCA=30°,
∴∠ACD=90°,
∴AC=![]()
在Rt△ACN中,∵AC=![]() ,∠ACN=∠DAC=30°,
,∠ACN=∠DAC=30°,
∴AN=![]() AC=
AC=![]()
∵AE=EH,GF=FH,
∴EF=![]() AG,
AG,
∵點G在BC上,∴AG的最大值為AC的長,最小值為AN的長,
∴AG的最大值為![]() ,最小值為
,最小值為![]() ,
,
∴EF的最大值為![]() ,最小值為
,最小值為![]() ,
,
∴EF的最大值與最小值的差為:![]()
故選:C


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
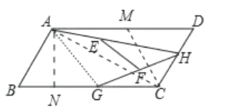
【題目】如圖,在![]() 中,點
中,點![]() 是
是![]() 的中點,點
的中點,點![]() 是線段
是線段![]() 的延長線上的一動點,連接
的延長線上的一動點,連接![]() ,過點
,過點![]() 作
作![]() 的平行線
的平行線![]() ,與線段
,與線段![]() 的延長線交于點
的延長線交于點![]() ,連接
,連接![]() 、
、![]() .
.

![]() 求證:四邊形
求證:四邊形![]() 是平行四邊形.
是平行四邊形.
![]() 若
若![]() ,
,![]() ,則在點
,則在點![]() 的運動過程中:
的運動過程中:
①當![]() ________時,四邊形
________時,四邊形![]() 是矩形,試說明理由;
是矩形,試說明理由;
②當![]() ________時,四邊形
________時,四邊形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
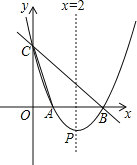
【題目】如圖,直線y=﹣x+3與x軸,y軸分別相交于點B,C,經過B,C兩點的拋物線y=ax2+bx+c與x軸的另一交點為A,頂點為P,且對稱軸是直線x=2.
(1)求該拋物線的函數表達式;
(2)請問在拋物線上是否存在點Q,使得以點B,C,Q為頂點的三角形為直角三角形?若存在,請求出點Q的坐標;若不存在,請說明理由;
(3)過S(0,4)的動直線l交拋物線于M,N兩點,試問拋物線上是否存在定點T,使得不過定點T的任意直線l都有∠MTN=90°?若存在,請求出點T的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校長暑假將帶領該校前級“三好學生”去北京大學游學,甲旅行社說:如果校長買全票一 張,則其余的學生可享受半價優惠.乙旅行社說:“包括校長在內全部按票價的六折優惠”. 若全票價為![]() 元,兩家旅行社的服務質量相同,根據三好學生的人數你認為選擇哪一 家旅行社才會比較合算?
元,兩家旅行社的服務質量相同,根據三好學生的人數你認為選擇哪一 家旅行社才會比較合算?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】作圖題:如圖,在平面直角坐標系中,△ABC的三個頂點坐標分別為A(﹣2,1),B(﹣1,4),C(﹣3,2).
(1)畫出△ABC關于y軸對稱的圖形△A1B1C1,并直接寫出C1點坐標;
(2)以原點O為位似中心,位似比為1:2,在y軸的左側,畫出△ABC放大后的圖形△A2B2C2,并直接寫出C2點坐標;
(3)如果點D(a,b)在線段AB上,請直接寫出經過(2)的變化后D的對應點D2的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】兩個反比例函數y=![]() (k>1)和y=
(k>1)和y=![]() 在第一象限內的圖象如圖所示,點P在y=
在第一象限內的圖象如圖所示,點P在y=![]() 的圖象上,PC⊥x軸于點C,交y=
的圖象上,PC⊥x軸于點C,交y=![]() 的圖象于點A,PD⊥y軸于點D,交y=
的圖象于點A,PD⊥y軸于點D,交y=![]() 的圖象于點B,BE⊥x軸于點E,當點P在y=
的圖象于點B,BE⊥x軸于點E,當點P在y=![]() 圖象上運動時,以下結論:①BA與DC始終平行;②PA與PB始終相等;③四邊形PAOB的面積不會發生變化;④△OBA的面積等于四邊形ACEB的面積.其中一定正確的是_____(填序號)
圖象上運動時,以下結論:①BA與DC始終平行;②PA與PB始終相等;③四邊形PAOB的面積不會發生變化;④△OBA的面積等于四邊形ACEB的面積.其中一定正確的是_____(填序號)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ACB=90°,∠BAC=40°,在直線AC上找點P,使△ABP是等腰三角形,則∠APB的度數為____________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了調查學生對垃圾分類及投放知識的了解情況,從甲、乙兩校各隨機抽取40名學生進行了相關知識測試,獲得了他們的成績(百分制),并對數據(成績)進行了整理、描述和分析.下面給出了部分信息.
a.甲、乙兩校40名學生成績的頻數分布統計表如下:

(說明:成績80分及以上為優秀,![]() 分為良好,
分為良好,![]() 分為合格,60分以下為不合格)
分為合格,60分以下為不合格)
b.甲校成績在![]() 這一組的是:70707071727373737475767778
這一組的是:70707071727373737475767778
c.甲、乙兩校成績的平均分、中位數、眾數如下:
學校 | 平均分(單位:分) | 中位數(單位:分) | 眾數(單位:分) |
甲 | 74.2 |
| 85 |
乙 | 73.5 | 76 | 84 |
根據以上信息,回答下列問題:
(1)上表中n的值為_____.
(2)在此次測試中,某學生的成績是74分,在他所屬學校排在前20名,由表中數據可知該學生是___校的學生(填“甲”或“乙”),請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com