議一議
(1)
正六邊形能否密鋪?簡述你的理由。(2)
分析圖，討論正五邊形不能密鋪的原因。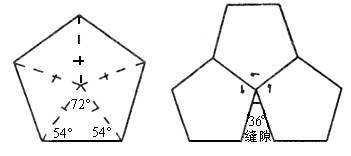
(3)
還能找到能密鋪的其他正多邊形嗎?通過上述問題的探討研究，可以看出對于給定的某種正多邊形，它能否拼成一個平面圖形，既不留下一絲空白，又不相互重疊，顯然與它的內角大小有關。為了探索哪些正多邊形能鋪滿平面，請根據圖，用計算器或量角器完成下表：
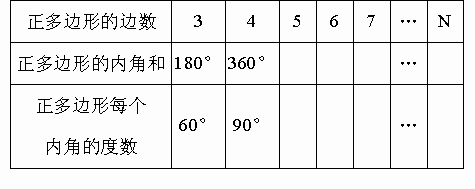
通過上面研討和計算，我們可以發現：當圍繞一點拼在一起的幾個多邊形的內角加在一起恰好組成一個周角時，就拼成一個平面圖形。
如正六邊形的每個內角為
120°，三個120°拼在一起恰好組成周角，所以全用正六邊形瓷磚就可以鋪滿地面。所以用相同的正多邊形拼地板或用兩種以上的正多邊形拼地板都可以達到密鋪的目的，甚至一些不規則的圖形也可以做到，如圖所示。
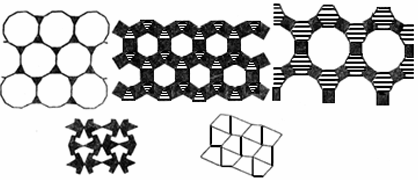
通過這節的學習，你學到了哪些知識，有哪些收獲，能否運用你所學過的知識試著完成下列問題。
科目：小學數學 來源： 題型：
如圖是一個梯形，當上底分別是6cm，4cm，2cm和1cm時，梯形的面積各是多少？查看答案和解析>>
科目：小學數學 來源： 題型：
于心在圓柱體的金魚缸的缸口貼了一圈裝飾花邊（見圖1）．她用正六邊形和等邊三角形按圖2的樣式進行密鋪．查看答案和解析>>
科目：小學數學 來源：創新版課程標準能力評估檢測叢書 數學 題型：042
| |||||||||||||||
查看答案和解析>>
科目：小學數學 來源：同步訓練與過關測試 小學數學 二年級 上冊) 題型：071
議一議：65－32這道題，小明用了如下幾種方法計算，你們能說出這些計算方法的思考過程嗎？
(1)60－30＝30 (2)65－30＝35
5－2＝3 35－2＝33
30＋3＝33
(3)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
