畫一個邊長3cm的正方形，并且在正方形內畫一個最大的圓：
①求出所畫圓的周長；
②如果剪去圓，剩下部分的面積是多少？
解：據分析解答如下：
以正方形的對角線為圓心，以正方形的邊長的一半為半徑，
畫圖如下：
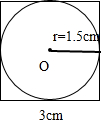
這個圓的周長是：3.14×3=9.42（厘米）；
剩余部分的面積是：3×3-3.14×（3÷2）
2，
=9-3.14×2.25，
=9-7.065，
=1.935（平方厘米）；
答：所畫圓的周長是9.42厘米；剩下部分的面積是1.935平方厘米．
分析：先畫出正方形，再依據圓的基本畫法，以正方形的對角線為圓心，以正方形的邊長的一半為半徑，即可畫出符合要求的圓，根據題意可知：這個圓的直徑就是正方形的邊長，再依據圓的周長和面積公式，即可得解．
點評：此題主要考查正方形內接圓的畫法以及面積的計算，關鍵是明確圓的直徑即為正方形的邊長．
名校課堂系列答案