Question

看圖求體積

（1）

 

；（2）

 

．

Answer 1

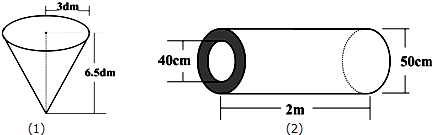
考點：圓錐的體積,圓柱的側面積、表面積和體積

專題：立體圖形的認識與計算

分析：（1）圓錐的底面半徑和高已知，利用圓錐的體積V=

1

3

Sh，即可求出這個圓錐的體積．
（2）此題也可以利用圓環柱的體積V=（S_外-S_內）h進行計算，先求出底面的面積，也就是圓環的面積，用大圓的面積減小圓的面積就是圓環的面積，再乘高即可．

解答： 解：（1）

1

3

×3.14×3²×6.5
=3.14×19.5
=61.23（立方分米）
答：圓錐的體積是61.23立方分米．

（3）50÷2=25（厘米）
40÷2=20（厘米）
2米=200厘米
3.14×（25²-20²）×200
=3.14×（625-400）×200
=3.14×225×200
=141300（立方厘米）
答：這個管道的體積是141300立方厘米．
故答案為：61.23立方分米，141300立方厘米．

點評：此題主要考查長方體的表面積和圓錐、圓柱的體積的計算方法．